
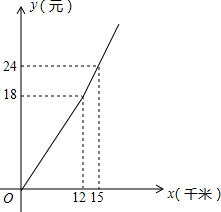
 随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )
随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.该打车方式采用阶梯收费标准.打车费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为20千米,则他的打车费用为( )| A. | 32元 | B. | 34元 | C. | 36元 | D. | 40元 |
分析 待定系数法求出x≥12时y关于x的函数解析式,再求出x=20时y的值即可.
解答 解:当行驶里程x≥12时,设y=kx+b,
将(12,18)、(15,24)代入,
得:$\left\{\begin{array}{l}{12k+b=18}\\{15k+b=24}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-6}\end{array}\right.$,
∴y=2x-6,
当x=20时,y=2×20-6=34,
∴如果小明某次打车行驶里程为20千米,则他的打车费用为34元;
故选:B.
点评 本题主要考查一次函数的图象与待定系数法求一次函数解析式,熟练掌握待定系数法求得一次函数解析式是解题的关键.


科目:初中数学 来源: 题型:填空题
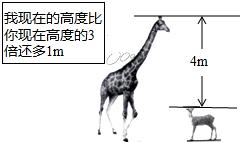 如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.
如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
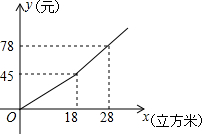 我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.
我国很多城市水资源缺乏,为了增强居民的节水意识,某市制定了每月用水18立方米以内(不含18立方米)和用水18立方米及以上两种收费标准(收费标准指每立方米水的价格),某用户每月应交水费y(元)是用水量x(立方米)的函数,其函数图象如图所示.| 用水量/立方米 | 水费/元 | |
| 小刚 | 15 | 37.5 |
| 小丽 | 25 | 68.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
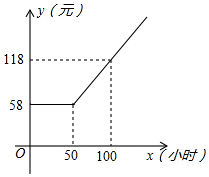 某广电局与长江证券公司联合推出光电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示.
某广电局与长江证券公司联合推出光电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
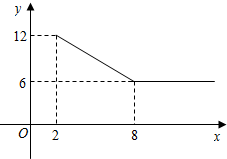 某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图所示;B类杨梅深加工后再销售,深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
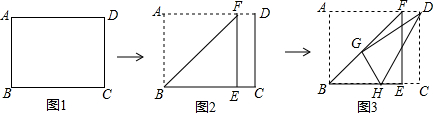
 如图,△ABC的中位线DE=10cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是16cm,则△ABC的面积为160cm2.
如图,△ABC的中位线DE=10cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是16cm,则△ABC的面积为160cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com