
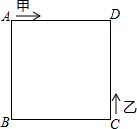
 如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若甲的速度是乙的速度的3倍,则它们第2017次相遇在边CD上.
如图,甲、乙两动点分别从正方形ABCD的顶点A,C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若甲的速度是乙的速度的3倍,则它们第2017次相遇在边CD上. 分析 根据甲、乙运动的方向结合速度间的关系即可得出甲、乙第1次相遇在边CD上、第2次相遇在边AD上、第3次相遇在边AB上、…,由此即可得出甲、乙相遇位置每四次一循环,再根据2017=504×4+1即可得出甲、乙第2017次相遇在边CD上.
解答 解:∵甲的速度是乙的速度的3倍,
∴甲、乙第1次相遇时,乙走了正方形周长的$\frac{1}{2}$×$\frac{1}{1+3}$=$\frac{1}{8}$,
∴甲、乙第1次相遇在边CD上.
∵甲的速度是乙的速度的3倍,甲点依顺时针方向环行,乙点依逆时针方向环行,
∴甲、乙第2次相遇在边AD上,甲、乙第3次相遇在边AB上,甲、乙第4次相遇在边BC上,甲、乙第5次相遇在边CD上,…,
∴甲、乙相遇位置每四次一循环.
∵2017=504×4+1,
∴甲、乙第2017次相遇在边CD上.
故答案为:CD.
点评 本题考查了规律型中数字的变化类,根据甲、乙运动的方向结合速度间的关系得出甲、乙相遇位置每四次一循环是解题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
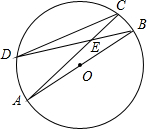 如图,AB是⊙O的直径,弦AC,BD交于点E,且tan∠AED=$\frac{1}{2}$,则$\frac{AB}{DC}$的值是$\frac{\sqrt{5}}{2}$.
如图,AB是⊙O的直径,弦AC,BD交于点E,且tan∠AED=$\frac{1}{2}$,则$\frac{AB}{DC}$的值是$\frac{\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 48 | B. | 60 | C. | 96 | D. | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
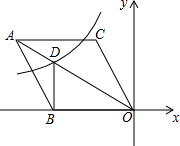 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,3$\sqrt{3}}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是-12$\sqrt{3}$.
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(-3,3$\sqrt{3}}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是-12$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com