
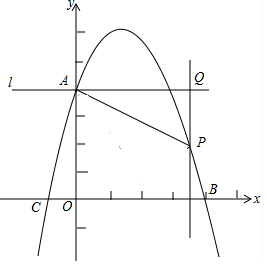
 已知抛物线y=-x2+3x+4交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l.在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
已知抛物线y=-x2+3x+4交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l.在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.分析 (1)先令x=0求出y的值即可得出A点坐标,再令y=0求出x的值即可得出BC两点的坐标;
(2)①分△AQP∽△AOC与△AQP∽△COA两种情况进行讨论;
②过点M作y轴的平行线交直线AQ于点E,过点P作PF⊥直线ME于点F,设Q(x,4),则P(x,-x2+3x+4),PQ=x2-3x=PM,再由△AEM∽△MFP求出PF的表达式,在Rt△AOM中根据勾股定理求出x的值,进而可得出P点坐标;
③根据在位于直线l下方的抛物线上任取一点P,而又点P位于抛物线的对称轴的右侧,则a>$\frac{3}{2}$,由点P在抛物线上即可建立m与n的关系.
解答 解:(1)∵令x=0,则y=4,
∴A(0,4);
∵令y=0,则-x2+3x+4=0,解得x1=4,x2=-1,
∴B(4,0),C(-1,0);
(2)①∵以A,P,Q三点构成的三角形与△AOC相似,
∴△AQP∽△AOC与△AQP∽△COA,
∴$\frac{AQ}{QP}=\frac{AO}{CO}$或$\frac{AQ}{QP}=\frac{CO}{AO}$,
即$\frac{x}{{x}^{2}-3x}=\frac{4}{1}$或$\frac{x}{{x}^{2}-3x}=\frac{1}{4}$,解得x=$\frac{13}{4}$或x=7,均在对称轴的右侧,
∴P($\frac{13}{4}$,$\frac{51}{16}$)或(7,-24);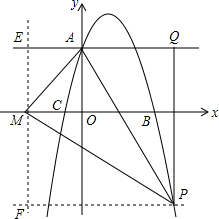
②如图所示,过点M作y轴的平行线交直线AQ于点E,过点P作PF⊥直线ME于点F,
设Q(x,4),则P(x,-x2+3x+4),PQ=x2-3x=PM,
∵∠EAM+∠EMA=90°,∠EMA+∠FMP=90°,
∴∠FMP=∠EAM.
∵∠MFP=∠AEM=90°,
∴△AEM∽△MFP,
∴$\frac{AM}{ME}=\frac{MP}{PF}$.
∵MP=x2-3x,
∴$\frac{x}{4}=\frac{{x}^{2}-3x}{PF}$,
∴PF=4x-12,
∴OM=(4x-12)-x=3x-12,
在Rt△AOM中,
∵OM2+OA2=AM2,即(3x-12)2+42=x2,解得x1=4,x2=5均在抛物线对称轴的右侧,
∴P(4,0)或(5,-6).
③∵抛物线y=-x2+3x+4和A(0,4),
∴抛物线和直线l的交点坐标为A(0,4),(3,4),
设P(a,-a2+3a+4);∵A(0,4),
∴把y=4代入y=-x2+3x+4中,得,x=0或x=3,
∴a>3
∵AP的中点是R,A(0,4),
∴$\frac{a}{2}$=m,$\frac{-{a}^{2}+3a+4+4}{2}$=n,
∴n=-2m2+3m+4,
∵a>3,
∴2m>3,
∴m>$\frac{3}{2}$.
点评 此题是二次函数综合题,主要涉及到相似三角形的判定与性质、二次函数图象上点的坐标特点及用待定系数法求二次函数的解析式等知识,在解答(2)时要分△AQP∽△AOC与△AQP∽△COA两种情况进行讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
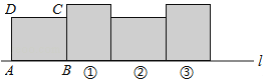 在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是3024π.
在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2016次后,顶点A在整个旋转过程中所经过的路程之和是3024π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
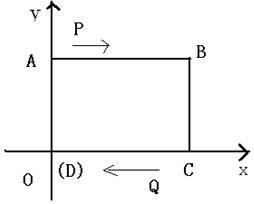 如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com