
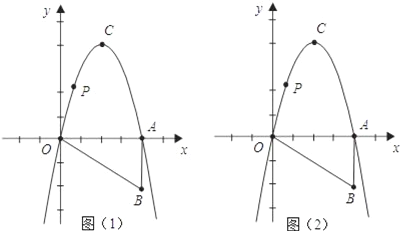
����Ŀ����ͼ��Rt��OAB��ͼ��ʾ������ƽ��ֱ������ϵ�У�ֱ�DZ�OA��x���غϣ���OAB=90�㣬OA=4��AB=2����Rt��OAB�Ƶ�O��ʱ����ת90�㣬��B��ת����C��λ�ã�һ�����������þ�����O��C��A���㣮
��1����������ߵĽ���ʽ��
��2����x���Ϸ�������������һ����P������P��x���ƽ���߽��������ڵ�M���ֱ����P����M��x��Ĵ��ߣ���x����E��F���㣬�ʣ��ı���PEFM���ܳ��Ƿ������ֵ������У��������ֵ����д�������̣����û�У���˵�����ɣ�
��3�����x������һ����H�������������Ƿ���ڵ�N��ʹO��ԭ�㣩��C��H��N�ĵ㹹����OCΪһ�ߵ�ƽ���ı��Σ������ڣ����N������ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1)��y=��x2+4x��(2)��10��(3)��N1��2+2![]() ����4����N2��2��2
����4����N2��2��2![]() ����4��
����4��
�����������������(1)��������ת�����ʿ����C�������A�����꣬����Ϊ�����߾���ԭ�㣬����y=ax2+bx�ѣ�2��4������4��0�����룬���a��b��ֵ��������������ߵĽ���ʽ��(2)���ı���PEFM���ܳ������ֵ�����P������ΪP��a����a2+4a�����������ߵĶԳ���֪OE=AF������EF=PM=4��2a��PE=MF=��a2+4a�������PEFM���ܳ�L=2[4��2a+����a2+4a��]=��2��a��1��2+10�����ú��������ʼ�������ı���PEFM���ܳ������ֵ��(3)�����������ϴ��ڵ�N��ʹO��ԭ�㣩��C��H��N�ĵ㹹����OCΪһ�ߵ�ƽ���ı��Σ��ɣ�1������������ߵĶ������꣬����C��x���ƽ���ߣ���x��û���������㣬��y=��4��x���ƽ���ߣ������������������㣬����������Ϊ�����N��������������x2+4x=��4���ⷽ�̼�������������꣮
���������(1)����ΪOA=4��AB=2������AOB�Ƶ�O��ʱ����ת90����
����ȷ����C������Ϊ��2��4������ͼ��֪��A������Ϊ��4��0����
����Ϊ�����߾���ԭ�㣬����y=ax2+bx�ѣ�2��4������4��0�����룬��![]() �����
�����![]()
���������ߵĽ���ʽΪy=��x2+4x��
(2)���ı���PEFM���ܳ������ֵ���������£�
�����⣬��ͼ��ʾ�����P������ΪP��a����a2+4a�����������ߵĶԳ���֪OE=AF��
��EF=PM=4��2a��PE=MF=��a2+4a��
�����PEFM���ܳ�L=2[4��2a+����a2+4a��]=��2��a��1��2+10��
����a=1ʱ������PEFM���ܳ������ֵ��Lmax=10��
(3)�����������ϴ��ڵ�N��ʹO��ԭ�㣩��C��H��N�ĵ㹹����OCΪһ�ߵ�ƽ���ı��Σ��������£�
��y=��x2+4x=����x��2��2+4��֪�������꣨2��4����
��֪��C�������Ƕ������֪꣬��C�㵽x��ľ���Ϊ4����λ���ȣ�
����C��x���ƽ���ߣ���x��û���������㣬��y=��4��x���ƽ���ߣ������������������㣬
���������������N��������������x2+4x=��4 ���x1=2+![]() ��x2=2��
��x2=2��![]()
��N������ΪN1��2+![]() ����4����N2��2��
����4����N2��2��![]() ����4����
����4����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
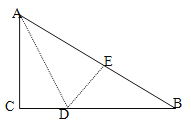
����Ŀ����ͼ����Rt��ABC�У���C=90������ACD��AD�۵���ʹ�õ�C����б��AB�ϵĵ�E����
��1����֤����BDE�ס�BAC��
��2����֪AC=6��BC=8�����߶�AD�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵ�һ������̨����һ������AB��һ���ܰ�AC�ͻ��ۣ����ƿ��ȣ���Ϊ��A����ɣ������ʾ��ͼΪ��ABC�����AC��BC��AB=5cm��AC=4cm����Ϊ����д���·��㣬�����̨���İڷţ��ƶ���C��C�䣬����C��=30��ʱ�����ƶ��ľ��뼴CC��ij������ü��������㣬���ȡ����������![]() =1.732��
=1.732�� ![]() =4.583��
=4.583��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȥ������ȷ���ǣ� ��
A.����2a+b��c��=2a+b��c
B.��2��a+b��4c��=��2a��2b+8c
C.������a��b+2c��=��a+b+2c
D.����a��b��c��=��a+b��c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫʹ��ʽ��x��y��2+M=��x+y��2��������ʽMӦ�ǣ�������
A. 2xy B. 4xy C. ��4xy D. ��2xy
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1������2��3+�� ![]() ����2��22������2��0
����2��22������2��0
��2��5x2y�£��� ![]() xy��3xy2 ��
xy��3xy2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���������������ļ�ֵ�����ݽ�������ѧУ��30������ѡ�ֵijɼ������˷���ͳ�ƣ�������±���
����x���֣� | 4��x��5 | 5��x��6 | 6��x��7 | 7��x��8 | 8��x��9 | 9��x��10 |
Ƶ�� | 2 | 6 | 8 | 5 | 5 | 4 |
���Ͽ�֪������ѡ�ַ�������λ�����ڵķ�����Ϊ��������
A. 5��x��6B. 6��x��7C. 7��x��8D. 8��x��9
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com