
分析 (1)首先找出公式中的a,b,c的值,再代入求根公式x═$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$求解即可;
(2)将原方程化为一般式,然后再找出公式中的a,b,c的值,再代入求根公式x═$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$求解即可;
(3)观察可得最简公分母是x(x-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答 解:(1)x2-2$\sqrt{5}$x=1,
x2-2$\sqrt{5}$x-1=0,
a=1,b=-2$\sqrt{5}$,c=-1,
△=b2-4ac=20+4=24,
x=$\frac{2\sqrt{5}±2\sqrt{6}}{2}$=$\sqrt{5}$±$\sqrt{6}$,
则:x1=$\sqrt{5}$-$\sqrt{6}$,x2=$\sqrt{5}$+$\sqrt{6}$;
(2)3x(x-1)=-x(x-1)+1,
3x2-3x=-x2+x+1,
4x2-4x-1=0,
a=4,b=-4,c=-1,
△=b2-4ac=16+16=32,
x=$\frac{4±4\sqrt{2}}{8}$=$\frac{1±\sqrt{2}}{2}$,
则:x1=$\frac{1-\sqrt{2}}{2}$,x2=$\frac{1+\sqrt{2}}{2}$;
(3)$\frac{2}{x}$+1=$\frac{2}{x-1}$方程的两边同乘x(x-1),得
2(x-1)+x(x-1)=2x,
2x-2+x2-x=2x,
x2-x-2=0,
(x-2)(x+1)=0,
解得x1=2,x2=-1.
检验:把x1=2,x2=-1代入x(x-1)都不等于0.
故原方程的解为:x1=2,x2=-1.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.同时考查了解分式方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第1排的座位数 | 第2排的座位数 | 第3排的座位数 | 第4排的座位数 | … |
| 24 | 24-x | 24-2x | 24-3x | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
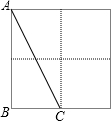 如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.
如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示的牌子上有两个整数“1和-1”,请你运用有关数学知识,用一句话对这两个整数进行描述(要求不能出现与牌子上相同的数字),请写出两种方案:
如图所示的牌子上有两个整数“1和-1”,请你运用有关数学知识,用一句话对这两个整数进行描述(要求不能出现与牌子上相同的数字),请写出两种方案:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com