
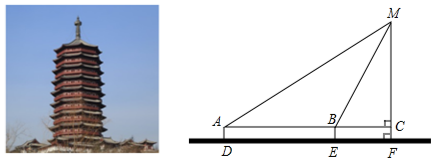
分析 设MC为xm,在Rt△BCM中,得到BC=$\frac{\sqrt{3}}{3}$x,在Rt△AMF中,得到AC=$\sqrt{3}$x,根据AC=AB+BC,列出方程即可解决问题.
解答 解:根据题意,得CF=BE=AD=1.5,AB=DE=40.
设MC为xm,在Rt△MCB中,tan∠1=$\frac{MC}{BC}$,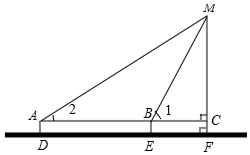
∴BC=$\frac{x}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
同理可得AC=$\sqrt{3}$x,
∴$\sqrt{3}$x=$\frac{\sqrt{3}}{3}$x+40,
解得$x=20\sqrt{3}≈34.64$.…(4分)
∴MF=MC+CF≈34.64+1.5=36.14≈36.1(m)
答:古塔的高约为36.1米.
点评 本题考查解直角三角形,仰角俯角的应用等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点,
以Rt△ABC的直角顶点C为圆心,作一圆切斜边AB于点T,过点A、B分别作⊙C的切线,E,D为切点,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
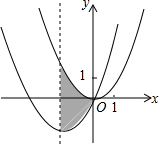 如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.
如图,抛物线C1:y=$\frac{1}{2}$x2经过平移得到抛物线C2:y=$\frac{1}{2}$x2+2x,抛物线C2的对称轴与两段抛物线所围成的阴影部分的面积是4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AC⊥BC,∠B=30°,点E,F是线段AC的三等分点,点P是线段BC上的动点,点Q是线段AC上的动点,若AC=3,则四边形EPQF周长的最小值是8.
如图,在△ABC中,AC⊥BC,∠B=30°,点E,F是线段AC的三等分点,点P是线段BC上的动点,点Q是线段AC上的动点,若AC=3,则四边形EPQF周长的最小值是8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com