
 解:(1)BE、PE、BF三条线段中任选两条.
解:(1)BE、PE、BF三条线段中任选两条.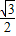 x,
x,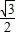 x2+2
x2+2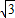 x.
x.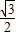 x2+2
x2+2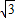 x
x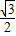 (x-2)2+2
(x-2)2+2 ,
,
 .
.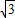 ;
;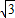 ;
;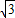 <r<2;
<r<2;

科目:初中数学 来源: 题型:
 如图,等边△ABC,G是△ABC的重心,直线AG把△ABC分成面积相等的两部分,但是不是过G点的任意一条直线都把△ABC分成面积相等的两部分?用实验或说理的方法,给予探索并得出结论.
如图,等边△ABC,G是△ABC的重心,直线AG把△ABC分成面积相等的两部分,但是不是过G点的任意一条直线都把△ABC分成面积相等的两部分?用实验或说理的方法,给予探索并得出结论.查看答案和解析>>
科目:初中数学 来源: 题型:
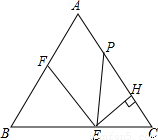
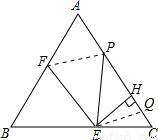
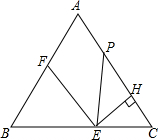 如图,等边△ABC边长为4,E是边BC上动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).
如图,等边△ABC边长为4,E是边BC上动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
(2012•渝北区一模)如图,等边△ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让△ABC沿这条直线向右平移,直到点B与点E重合为止,设BD的长为x,△ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com