
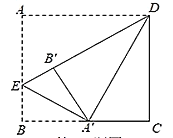
【题目】如图,在矩形![]() 中,
中,![]() .将
.将![]() 向内翻折,点
向内翻折,点 ![]() 落在
落在![]() 上,记为
上,记为![]() ,折痕为
,折痕为![]() .若将
.若将![]() 沿
沿![]() 向内翻折,点
向内翻折,点![]() 恰好 落在
恰好 落在![]() 上,记为
上,记为![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
首先根据矩形和翻折的性质得出△AED≌△A'ED,△A'BE≌△A'B'E,∠A'B'E=∠B=∠A'B'D=90°,∠AED=∠A'ED,∠A'EB=∠A'EB',BE=B'E,进而得出∠AED=∠A'ED=∠A'EB=60°,∠ADE=∠A'DE=∠A'DC=30°,判定△DB'A'≌△DCA',DC=DB',得出AE,设AB=DC=x,利用勾股定理构建方程,即可得解.
∵四边形ABCD为矩形,
∴∠ADC=∠C=∠B=90°,AB=DC,
由翻折知,△AED≌△A'ED,△A'BE≌△A'B'E,∠A'B'E=∠B=∠A'B'D=90°,
∴∠AED=∠A'ED,∠A'EB=∠A'EB',BE=B'E,
∴∠AED=∠A'ED=∠A'EB=![]() ×180°=60°,
×180°=60°,
∴∠ADE=90°﹣∠AED=30°,∠A'DE=90°﹣∠A'EB=30°,
∴∠ADE=∠A'DE=∠A'DC=30°,
又∵∠C=∠A'B'D=90°,DA'=DA',
∴△DB'A'≌△DCA'(AAS),
∴DC=DB',
在Rt△AED中,
∠ADE=30°,AD=2,
∴AE=![]() ,
,
设AB=DC=x,则BE=B'E=x﹣![]()
∵AE2+AD2=DE2,
∴(![]() )2+22=(x+x﹣
)2+22=(x+x﹣![]() )2,
)2,
解得,x1=![]() (负值舍去),x2=
(负值舍去),x2=![]() ,
,
故答案为B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AC=nAB,∠CAB=α,点E,F分别在AB,AC上且EF∥BC,把△AEF绕点A顺时针旋转到如图2的位置.连接CF,BE.

(1)求证:∠ACF=∠ABE;
(2)若点M,N分别是EF,BC的中点,当α=90°时,求证:BE2+CF2=4MN2;
(3)如图3,点M,N分别在EF,BC上且![]() =
=![]() =
=![]() ,若n=
,若n=![]() ,α=135°,BE=
,α=135°,BE=![]() ,直接写出MN的长.
,直接写出MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣4,﹣2),B(﹣2,﹣2),C(﹣1,0).

(1)将△ABC向右平移5个单位长度,画出平移后的△A1B1C1;
(2)将△ABC绕点C旋转180°,画出旋转后的△A2B2C,并直接写出点A运动的路径长;
(3)请直接写出△B1C1B2的外心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个转盘中指针落在每个数字上的机会相等,现同时转动![]() 、
、![]() 两个转盘,停止后,指针各指向一个数字.小力和小明利用这两个转盘做游戏,若两数之积为非负数则小力胜;否则,小明胜.
两个转盘,停止后,指针各指向一个数字.小力和小明利用这两个转盘做游戏,若两数之积为非负数则小力胜;否则,小明胜.
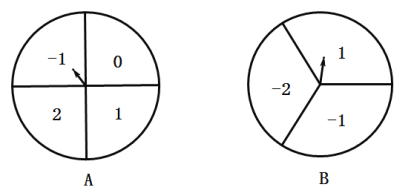
(1)画树状图或列表求出各人获胜的概率。
(2)这个游戏公平吗?说说你的理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD、AE,则∠EAD的度数为( )
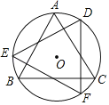
A.150°B.135°C.120°D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师提出问题:如图1,有一张长![]() ,宽
,宽![]()
![]() 的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成-一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.下 面是探究过程,请补充完整:
的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成-一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.下 面是探究过程,请补充完整:
(1)设小正方形的边长为![]() ,体积为
,体积为![]() ,根据长方体的体积公式得到
,根据长方体的体积公式得到![]() 和
和![]() 的关系式 ;
的关系式 ;
(2)确定自变量![]() 的取值范围是
的取值范围是
(3)列出![]() 与
与![]() 的几组对应值.
的几组对应值.

| ··· |
|
|
|
|
|
|
|
|
|
|
| ··· |
|
|
|
|
|
|
|
|
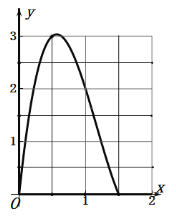
(4)在平面直角坐标系![]() 中,描出以补全后的表中各对对应值为坐标的点画出该函数的图象如图2,结合画出的函数图象,当小正方形的边长约为
中,描出以补全后的表中各对对应值为坐标的点画出该函数的图象如图2,结合画出的函数图象,当小正方形的边长约为 ![]() 时, 盒子的体积最大,最大值约为
时, 盒子的体积最大,最大值约为![]() .(估读值时精确到
.(估读值时精确到![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
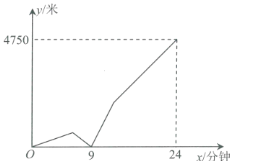
【题目】一天早上,王霞从家出发步行上学,出发6分钟后王霞想起数学作业没有带,王霞立即打电话叫爸爸骑自行车把作业送来(接打电话和爸爸出门的时间忽略不计),同时王霞把速度降低到前面的一半.爸爸骑自行车追上王霞后立即掉头以原速赶往位于家的另一边的单位上班,王霞拿到作业后立即改为慢跑上学,慢跑的速度是最开始步行速度的2倍,最后王霞比爸爸早10分钟到达目的地.如图反映了王霞与爸爸之间的距离![]() (米)与王霞出发后时间
(米)与王霞出发后时间![]() (分钟)之间的关系,则王霞的家距离学校有__________米.
(分钟)之间的关系,则王霞的家距离学校有__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节“赛龙舟,吃粽子”是中华民族的传统习俗.节日期间,小邱家包了三种不同馅的粽子,分别是:红枣粽子(记为A),豆沙粽子(记为B),肉粽子(记为C),这些粽子除了馅不同,其余均相同.粽子煮好后,小邱的妈妈给一个白盘中放入了两个红枣粽子,一个豆沙粽子和一个肉粽子;给一个花盘中放入了两个肉粽子,一个红枣粽子和一个豆沙粽子.
根据以上情况,请你回答下列问题:
(1)假设小邱从白盘中随机取一个粽子,恰好取到红枣粽子的概率是多少?
(2)若小邱先从白盘里的四个粽子中随机取一个粽子,再从花盘里的四个粽子中随机取一个粽子,请用列表法或画树状图的方法,求小邱取到的两个粽子中一个是红枣粽子、一个是豆沙粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() .(1)已知点
.(1)已知点![]() 在第一象限的抛物线上,则点
在第一象限的抛物线上,则点![]() 的坐标是_______.(2)在(l)的条件下连接
的坐标是_______.(2)在(l)的条件下连接![]() ,
,![]() 为抛物线上一点且
为抛物线上一点且![]()
![]() ,则点
,则点![]() 的坐标是_______.
的坐标是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com