
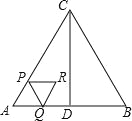
ĄŸÌâÄżĄżÈçÍŒŁŹĄśABCÊǔȱßÈęœÇĐÎŁŹAB=4cmŁŹCDĄÍABÓÚ”ăDŁŹ¶Ż”ăPŽÓ”ăAłö·ąŁŹŃŰACÒÔ2cm/s”ÄËÙ¶ÈÏòÖŐ”ăCÔ˶ŻŁŹ”±”ăPłö·ąșóŁŹčę”ăPŚśPQĄÎBCœ»ŐÛÏßAD©DCÓÚ”ăQŁŹÒÔPQÎȘ±ßŚś”ȱßÈęœÇĐÎPQRŁŹÉèËıßĐÎAPRQÓ륜ACDÖŰ”țČż·ÖÍŒĐΔÄĂæ»ęÎȘSŁšcm2Ł©ŁŹ”ăPÔ˶Ż”ÄʱŒäÎȘtŁšsŁ©Łź
Łš1Ł©”±”ăQÔÚÏ߶ÎADÉÏʱŁŹÓĂșŹt”ÄŽúÊęÊœ±íÊŸQR”Äł€Ł»
Łš2Ł©Çó”ăRÔ˶Ż”Ä·łÌł€Ł»
Łš3Ł©”±”ăQÔÚÏ߶ÎADÉÏʱŁŹÇóSÓëtÖźŒä”ÄșŻÊęčŰϔʜŁ»
Łš4Ł©Ö±œÓĐŽłöÒÔ”ăBĄąQĄąRÎȘ¶„”ă”ÄÈęœÇĐÎÊÇÖ±œÇÈęœÇĐÎʱt”ÄÖ”Łź
ĄŸŽđ°žĄżŁš1Ł©Ö€ĂśŒûœâÎöŁš2Ł©2![]() +2Łš3Ł©ąÙS=SÁâĐÎAPRQ2
+2Łš3Ł©ąÙS=SÁâĐÎAPRQ2![]() t2Ł»ąÚS=©
t2Ł»ąÚS=©![]() t2+6
t2+6![]() t©2
t©2![]() Łš4Ł©t=
Łš4Ł©t=![]() »òt=
»òt=![]()
ĄŸœâÎöĄż
ÊÔÌâ·ÖÎöŁșŁš1Ł©ÒŚÖ€ĄśAPQÊǔȱßÈęœÇĐÎŁŹŒŽżÉ”Ă”œQR=PQ=AP=2tŁ»
Łš2Ł©čę”ăAŚśAGĄÍBCÓÚ”ăGŁŹÈçÍŒąÚŁŹÒŚ”Ă”ăRÔ˶Ż”Ä·łÌł€ÊÇAG+CGŁŹÖ»ĐèÇółöAGĄąCGŸÍżÉœâŸöÎÊÌ⣻
Łš3Ł©ËıßĐÎAPRQÓ륜ACDÖŰ”țČż·ÖÍŒĐÎżÉÄÜÊÇÁâĐÎŁŹÒČżÉÄÜÊÇÎć±ßĐÎŁŹčÊĐè·ÖÇéżöÌÖÂÛŁŹÈ»șóÔËÓĂžîČč·šŸÍżÉœâŸöÎÊÌ⣻
Łš4Ł©ÓÉÓÚÖ±œÇ¶„”ăČ»È·¶šŁŹčÊĐè·ÖÇéżöÌÖÂÛŁŹÖ»Đè·ÖĄÏQRB=90ĄășÍĄÏRQB=90ĄăÁœÖÖÇéżöÌÖÂÛŁŹŒŽżÉœâŸöÎÊÌ⣟
ÊÔÌâœâÎöŁșŁš1Ł©ÈçÍŒąÙŁŹ

ĄßĄśABCÊǔȱßÈęœÇĐÎŁŹ
ĄàĄÏACB=ĄÏB=60ĄăŁź
ĄßPQĄÎBCŁŹ
ĄàĄÏAPQ=ĄÏACB=60ĄăŁŹĄÏAQP=ĄÏB=60ĄăŁŹ
ĄàĄśAPQÊǔȱßÈęœÇĐÎŁź
ĄàPQ=AP=2tŁź
ĄßĄśPQRÊǔȱßÈęœÇĐÎŁŹ
ĄàQR=PQ=2tŁ»
Łš2Ł©čę”ăAŚśAGĄÍBCÓÚ”ăGŁŹÈçÍŒąÚŁŹ

Ôò”ăRÔ˶Ż”Ä·łÌł€ÊÇAG+CGŁź
ÔÚRtĄśAGCÖĐŁŹĄÏAGC=90ĄăŁŹsin60Ąă=![]() ŁŹcos60Ąă=
ŁŹcos60Ąă=![]() ŁŹAC=4ŁŹ
ŁŹAC=4ŁŹ
ĄàAG=2![]() ŁŹCG=2Łź
ŁŹCG=2Łź
Ąà”ăRÔ˶Ż”Ä·łÌł€2![]() +2Ł»
+2Ł»
Łš3Ł©ąÙ”±0ŁŒtĄÜ![]() ʱŁŹÈçÍŒąÛŁŹ
ʱŁŹÈçÍŒąÛŁŹ

S=SÁâĐÎAPRQ=2ĄÁSŐ꥜APQ=2ĄÁ![]() ĄÁŁš2tŁ©2=2
ĄÁŁš2tŁ©2=2![]() t2Ł»
t2Ł»
ąÚ”±![]() ŁŒtĄÜ1ʱŁŹÈçÍŒąÜ
ŁŒtĄÜ1ʱŁŹÈçÍŒąÜ

PE=PCsinĄÏPCE=Łš4©2tŁ©ĄÁ![]() =2©tŁŹ
=2©tŁŹ
ĄàER=PR©PE=2t©Łš2©tŁ©=3t©2ŁŹ
ĄàEF=ERtanR=![]() Łš3t©2Ł©
Łš3t©2Ł©
ĄàS=SÁâĐÎAPRQ©SĄśREF
=2![]() t2©
t2©![]() Łš3t©2Ł©2=©
Łš3t©2Ł©2=©![]() t2+6
t2+6![]() t©2
t©2![]() Ł»
Ł»
Łš4Ł©t=![]() »òt=
»òt=![]()
ÌáÊŸŁșąÙ”±ĄÏQRB=90ĄăʱŁŹÈçÍŒąĘŁŹ

cosĄÏRQB=![]() ŁŹ
ŁŹ
ĄàQB=2QR=2QAŁŹ
ĄàAB=3QA=6t=4ŁŹ
Ąàt=![]() Ł»
Ł»
ąÚ”±ĄÏRQB=90ĄăʱŁŹÈçÍŒąȚŁŹ

ÍŹÀíżÉ”ĂBC=3RC=3PC=3Łš4©2tŁ©=4ŁŹ
Ąàt=![]() Łź
Łź


 ĂûĐŁĂûÊŠĆàÓĆŚśÒ”±ŸŒÓșËĐÄÊÔŸíÏ”ÁĐŽđ°ž
ĂûĐŁĂûÊŠĆàÓĆŚśÒ”±ŸŒÓșËĐÄÊÔŸíÏ”ÁĐŽđ°ž È«łÌœđŸíÏ”ÁĐŽđ°ž
È«łÌœđŸíÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłĐŁÓûŐĐÆžÒ»ĂûÊęѧœÌÊŠŁŹŃ§ĐŁ¶ÔŒŚĄąÒÒĄą±ûÈęλșòŃĄÈËœűĐĐÁËÈęÏîÄÜÁŠČâÊÔŁŹžśÏîČâÊÔłÉŒšÂú·ÖŸùÎȘ100·ÖŁŹžùŸĘœáčûÔńÓĆÂŒÓĂŁźÈęλșòŃĄÈ˔ĞśÏîČâÊÔłÉŒšÈçϱíËùÊŸŁș
ČâÊÔÏîÄż | |||
ČâÊÔłÉŒš/·Ö | |||
ŒŚ | ÒÒ | ±û | |
œÌѧÄÜÁŠ | 85 | 73 | 73 |
żÆŃĐÄÜÁŠ | 70 | 71 | 65 |
ŚéÖŻÄÜÁŠ | 64 | 72 | 84 |
(1)ÈçčûžùŸĘÈęÏîČâÊÔ”ÄÆœŸùłÉŒšŁŹËœ«±»ÂŒÓĂŁŹË”ĂśÀíÓÉŁ»
(2)žùŸĘÊ”ŒÊĐèÒȘŁŹŃ§ĐŁœ«œÌѧĄążÆŃĐșÍŚéÖŻÈęÏîÄÜÁŠČâÊԔ÷ְŽ5ĄĂ3ĄĂ2”ıÈÀęÈ·¶šĂżÈË”ÄłÉŒšŁŹËœ«±»ÂŒÓĂŁŹË”ĂśÀíÓÉŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÓĂżÆѧŒÇÊę·š±íÊŸÏÂÁĐžśÊęŁș
1Íò=
1ÒÚ=
80000000=
-76500000=
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłĐŁÎȘÁ˷ុѧÉú”ĔڶțżÎÌĂŁŹ¶ÔѧÉúČÎÓëŃĘœČĄąÎ蔞ĄąÊé·šșÍÉăÓ°»î¶Ż”ÄĐËÈ€ÇéżöœűĐĐ”śČ飏ѧУČÉÈĄËæ»úłéŃù”Ä·œ·šœűĐĐÎÊŸí”śČ飚ÿžö±»”śČé”ÄѧÉú±ŰĐëŃĄÔń¶űÇÒÖ»ÄÜŃĄÔńÆäÖĐŚîžĐĐËÈ€”ÄÒ»ÏŁŹ¶Ô”śČéœáčûœűĐĐÍłŒÆșóŁŹ»æÖÆÁËÈçÏÂÁœžöÍłŒÆÍŒŁș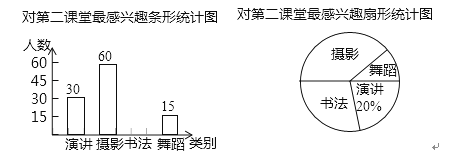
Łš1Ł©ŽËŽÎ”śČéłéÈĄ”ÄѧÉúÈËÊęm= ĄĄĂûŁŹÆäÖĐŃĄÔńĄ°Êé·šĄ±”ÄѧÉúŐŒłéŃùÈËÊę”Ä°Ù·Ö±Èn=ĄĄ Ł»
Łš2Ł©ÈôžĂĐŁÓĐ3000ĂûѧÉúŁŹÇëžùŸĘÒÔÉÏÊęŸĘčÀŒÆžĂĐŁ¶ÔĄ°Êé·šĄ±ŚîžĐĐËÈ€”ÄѧÉúÈËÊ꣟
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘŁșÔÚRtĄśABCÖĐŁŹĄÏC=90ĄăĄÏAĄąĄÏBĄąĄÏCËù¶Ô”ı߷ֱđŒÇŚśaĄąbĄącŁź
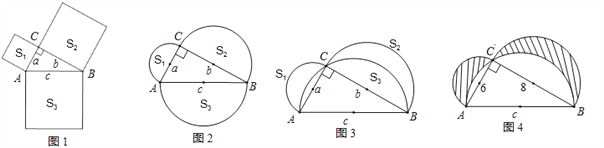
Łš1Ł©ÈçÍŒ1ŁŹ·Ö±đÒÔĄśABC”ÄÈęÌő±ßÎȘ±ßł€ÏòÍ⌜Őę·œĐÎŁŹÆäŐę·œĐΔÄĂæ»ęÓÉĐĄ”œŽó·Ö±đŒÇŚśS1ĄąS2ĄąS3ŁŹÔòÓĐ____________Ł»
Łš2Ł©ÈçÍŒ2ŁŹ·Ö±đÒÔĄśABC”ÄÈęÌő±ßÎȘÖ±Ÿ¶ÏòÍ⌜°ëÔČŁŹÆä°ëÔČ”ÄĂæ»ęÓÉĐĄ”œŽó·Ö±đŒÇŚśS1ĄąS2ĄąS3ŁŹÇëÎÊS1+S2ÓëS3ÓĐÔőŃù”ÄÊęÁżčŰÏ”ŁŹČąÖ€ĂśÄă”ÄœáÂÛŁ»
Łš3Ł©·Ö±đÒÔÖ±œÇÈęœÇĐΔÄÈęÌő±ßÎȘÖ±Ÿ¶Śś°ëÔČŁŹÈçÍŒ3ËùÊŸŁŹÆäĂæ»ęÓÉĐĄ”œŽó·Ö±đŒÇŚśS1ĄąS2ĄąS3ŁŹžùŸĘŁš2Ł©ÖĐ”ÄÌœËśŁŹÖ±œÓ»ŰŽđS1+S2ÓëS3ÓĐÔőŃù”ÄÊęÁżčŰÏ”Ł»
Łš4Ł©ÈôRtĄśABCÖĐŁŹAC=6ŁŹBC=8ŁŹÇółöÍŒ4ÖĐÒőÓ°Čż·Ö”ÄĂæ»ęŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżĐĄĂśœâ·œłÌ![]() ”ÄčęłÌÈçÏÂŁźÇëÖžłöËûœâŽđčęłÌÖДĎíÎóŁŹČąĐŽłöŐęÈ·”ÄœâŽđčęłÌŁź
”ÄčęłÌÈçÏÂŁźÇëÖžłöËûœâŽđčęłÌÖДĎíÎóŁŹČąĐŽłöŐęÈ·”ÄœâŽđčęłÌŁź
œâŁș·œłÌÁœ±ßÍŹłËxŁŹ”Ă1Ł(xŁ2)Łœ1.ĄĄąÙ
È„ÀšșĆŁŹ”Ă1ŁxŁ2Łœ1.ĄĄąÚ
șÏȹ͏ÀàÏ”ĂŁxŁ1Łœ1.ĄĄąÛ
ÒÆÏ”ĂŁxŁœ2.ĄĄąÜ
œâ”ĂxŁœŁ2.ĄĄąĘ
ĄàÔ·œłÌ”ÄœâÎȘxŁœŁ2.ĄĄąȚ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚx=©4ŁŹ©1ŁŹ0ŁŹ3ÖĐŁŹÂúŚăČ»”ÈÊœŚé![]() ”ÄxÖ”ÊÇŁšĄĄĄĄŁ©
”ÄxÖ”ÊÇŁšĄĄĄĄŁ©
A.©4șÍ0
B.©4șÍ©1
C.0șÍ3
D.©1șÍ0
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚÖ±œÇŚű±êÏ”ÖĐŁŹĄŃCčęÔ”ăOŁŹœ»xÖáÓÚ”ăAŁš2ŁŹ0Ł©ŁŹœ»yÖáÓÚ”ăBŁš0ŁŹ![]() Ł©Łź
Ł©Łź
Łš1Ł©ÇóÔČĐÄC”ÄŚű±êŁź
Łš2Ł©ĆŚÎïÏßy=ax2+bx+cčęOŁŹAÁœ”㣏ÇÒ¶„”ăÔÚŐę±ÈÀęșŻÊęy=-![]() ”ÄÍŒÏóÉÏŁŹÇóĆŚÎïÏߔĜâÎöÊœŁź
”ÄÍŒÏóÉÏŁŹÇóĆŚÎïÏߔĜâÎöÊœŁź
Łš3Ł©čęÔČĐÄCŚśÆœĐĐÓÚxÖá”ÄÖ±ÏßDEŁŹœ»ĄŃCÓÚDŁŹEÁœ”㣏ÊÔĆжÏDŁŹEÁœ”ăÊÇ·ńÔÚŁš2Ł©ÖĐ”ÄĆŚÎïÏßÉÏŁź
Łš4Ł©ÈôŁš2Ł©ÖĐ”ÄĆŚÎïÏßÉÏŽæÔÚ”ăPŁšx0ŁŹy0Ł©ŁŹÂúŚăĄÏAPBÎȘ¶ÛœÇŁŹÇóx0”ÄÈĄÖ”·¶Î§Łź

Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com