
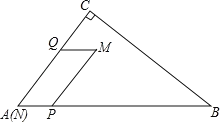
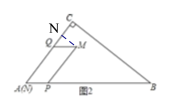
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位的速度向终点
以每秒1个单位的速度向终点![]() 运动;同时,点
运动;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位的速度向终点
以每秒2个单位的速度向终点![]() 运动,当
运动,当![]() 、
、![]() 两点其中一点到达点
两点其中一点到达点![]() 时,另一点也随之停止运动,过点
时,另一点也随之停止运动,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() .当点
.当点![]() 与点
与点![]() 不重合时,以
不重合时,以![]() 、
、![]() 为邻边作
为邻边作![]() .设
.设![]() 、
、![]() 两点的运动时间为
两点的运动时间为![]() 秒.
秒.
(1)求线段![]() 的长.(用含
的长.(用含![]() 的代数式表示)
的代数式表示)
(2)点![]() 在边
在边![]() 上运动,当点
上运动,当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值.
的值.
(3)设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,当点
,当点![]() 在
在![]() 内部时,求
内部时,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当![]() 的一边是它邻边2倍时,直接写出
的一边是它邻边2倍时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;(2)
;(2)![]() ;(3)
;(3)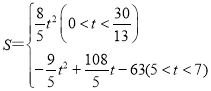 ;(4)
;(4)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)分两种情况:当![]() 时,点
时,点![]() 在线段
在线段![]() 上运动,当
上运动,当![]() 时,点
时,点![]() 在线段
在线段![]() 上运动,分别求出CQ的长,即可;
上运动,分别求出CQ的长,即可;
(2)当点![]() 落在边
落在边![]() 上时,易得
上时,易得![]() ,结合四边形
,结合四边形![]() 是平行四边形,列出方程,即可求解;
是平行四边形,列出方程,即可求解;
(3)分两种情况:①当![]() 时,过点M作MN⊥AC于点N,②当
时,过点M作MN⊥AC于点N,②当![]() 时,过点Q作QH⊥AB于点H,分别求出S关于t的解析式,即可;
时,过点Q作QH⊥AB于点H,分别求出S关于t的解析式,即可;
(4)分两种情况:①当![]() 时,
时,![]() 在线段
在线段![]() 上运动,
上运动,![]() ②当点
②当点![]() 在线段
在线段![]() 上运动时,根据
上运动时,根据![]() 或
或![]() ,列方程,求出t的值,进而即可得到t的范围.
,列方程,求出t的值,进而即可得到t的范围.
(1)∵在![]() 中,
中,![]() ,
,
∴当![]() 时,点
时,点![]() 在线段
在线段![]() 上运动,
上运动,![]() ,
,
当![]() 时,点
时,点![]() 在线段
在线段![]() 上运动,
上运动,![]() ;
;
(2)∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
当点![]() 落在边
落在边![]() 上时,如图1,
上时,如图1,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() ,
,
解得:![]() ;
;
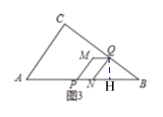
(3)①当![]() 时,点
时,点![]() 在
在![]() 内部,过点M作MN⊥AC于点N,如图2,则∠QNM=∠C=90°,
内部,过点M作MN⊥AC于点N,如图2,则∠QNM=∠C=90°,
∵![]() ,
,
∴∠MQN=∠A,
![]()
![]() ,
,
∴MN=![]() QM=
QM=![]() AP=
AP=![]() t,
t,
∴![]() ,
,
∵当t=5时,点M与点Q重合,
∴②当![]() 时,点
时,点![]() 在
在![]() 内部,过点Q作QH⊥AB于点H,如图3,
内部,过点Q作QH⊥AB于点H,如图3,
∵QN∥PM∥AC,
![]()
![]() ,即:NB=
,即:NB=![]() QB=
QB=![]() (10-2t),
(10-2t),
∴PN=10-AP-BN=![]() ,
,
同理:QH=![]() ,
,
∴![]() ,
,
综上所述:![]() 与
与![]() 之间的函数关系式为:
之间的函数关系式为: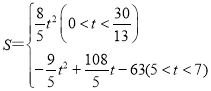 ;
;
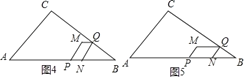
(4)①当![]() 时,
时,![]() 在线段
在线段![]() 上运动,即
上运动,即![]() ,
,
![]()
②如图4,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() ,
,
∵![]()
![]() ,即:QN=
,即:QN=![]() ,
,
∴PM=QN=![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
如图5,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴当![]() 的一边是它邻边2倍时,
的一边是它邻边2倍时,![]() 的取值范围为:
的取值范围为:![]() 或
或![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
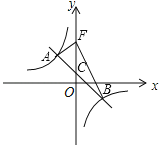
【题目】在平面直角坐标系中,一次函数y=﹣x+b的图象与反比例函数y=![]() (k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(k≠0)的图象交于A、B点,与y轴交于点C,其中点A的半标为(﹣2,3)
(1)求一次函数和反比例函数的解析式;
(2)如图,若将点C沿y轴向上平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
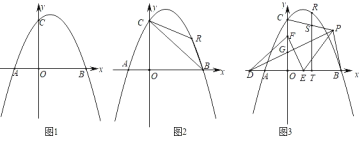
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师在讲解复习《圆》的内容时,用投影仪屏幕展示出如下内容:
如图,![]() 内接于
内接于![]() ,直径
,直径![]() 的长为2,过点
的长为2,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
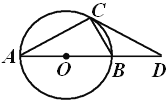
张老师让同学们添加条件后,编制一道题目,并按要求完成下列填空.
(1)在屏幕内容中添加条件![]() ,则
,则![]() 的长为______.
的长为______.
(2)以下是小明、小聪的对话:
小明:我加的条件是![]() ,就可以求出
,就可以求出![]() 的长
的长
小聪:你这样太简单了,我加的是![]() ,连结
,连结![]() ,就可以证明
,就可以证明![]() 与
与![]() 全等.
全等.
参考上面对话,在屏幕内容中添加条件,编制一道题目(此题目不解答,可以添线、添字母).______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
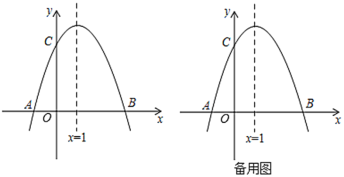
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() (
(![]() )秒.若
)秒.若![]() 与
与![]() 相似,请求出
相似,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车准备从甲地开往乙地.若平均速度为80km/h,则需要5h到达.
(1)写出汽车从甲地到乙地所用时间![]() 与平均速度
与平均速度![]() 之间的关系式;
之间的关系式;
(2)如果准备用8h到达,那么平均速度是多少?
(3)已知汽车的最大平均速度是100km/h,那么汽车最少用多长时间可以到达?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了以“不忘初心,牢记使命”为主题的知识竞赛,现从该校八、九年级各随机抽取10名学生的成绩进行整理,描述和分析(成绩用m表示),共分成四个组:A.80≤m<85,B.85≤m<90,C.90≤m<95,D.95≤m≤100.另外给出了部分信息如下:
八年级10名学生的成绩:99,80,99,86,99,96,90,100,89,82.
九年级10名学生的成绩在C组的数据:94,90,94.
八、九年级抽取学生成绩统计表 | ||
年级 | 八年级 | 九年级 |
平均数 | 92 | 92 |
中位数 | 93 | b |
众数 | c | 100 |
方差 | 52 | 50.4 |
根据以上信息,解答下列问题:
(1)上面图表中的a= ,b= ,c= .
(2)扇形统计图中“D组”所对应的圆心角的度数为 .
(3)根据以上信息,你认为哪个年级的学生对“不忘初心,牢记使命”的内容掌握较好?说明理由.(一条即可)
(4)该校九年级共有840名学生参加了知识竞赛活动,估计九年级参加此次知识竞赛活动成绩为较好(90≤m<95)的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平行四边形![]() 在平面直角坐标系中,
在平面直角坐标系中,![]() (点
(点![]() 在点
在点![]() 的左侧)两点的横坐标是方程
的左侧)两点的横坐标是方程![]() 的两个根,点
的两个根,点![]() 在
在![]() 轴上,其中
轴上,其中![]() .
.
![]() 若
若![]() 是第一象限位于直线
是第一象限位于直线![]() 上方的一点,过
上方的一点,过![]() 作
作![]() 于
于![]() 过
过![]() 作
作![]() 轴于
轴于![]() 点,作
点,作![]() 轴交直线
轴交直线![]() 于
于![]() 为
为![]() 中点,其中
中点,其中![]() 的周长是
的周长是![]() ;若
;若![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 为直线
为直线![]() 上一动点,连接
上一动点,连接![]() ,求
,求![]() 的最小值,此时
的最小值,此时![]() 轴上有一个动点
轴上有一个动点![]() ,当
,当![]() 最大时,求
最大时,求![]() 点坐标;
点坐标;
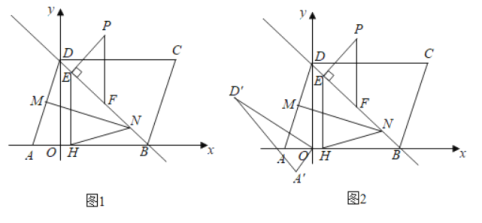
![]() 在
在![]() 的情况下,将
的情况下,将![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 后得到
后得到![]() 如图2,将线段
如图2,将线段![]() 沿着
沿着![]() 轴平移记平移过程中的线段
轴平移记平移过程中的线段![]() 为
为![]() ,在平面直角坐标系中是否存在点
,在平面直角坐标系中是否存在点![]() ,使得以点
,使得以点![]() 为顶点的四边形为菱形,若存在,请求出点
为顶点的四边形为菱形,若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查过程如下,请补充完整,
收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试测试成绩(百分制)如下:
甲班:65,75,75,80,60,50,75,90,85,65
乙班:90,55,80,70,55,70,95,80,65,70
(1)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x人数班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=________;n=________.
(2)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 75 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=________,y=________.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀请估计乙班50名学生中身体素质为优秀的学生有________人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com