
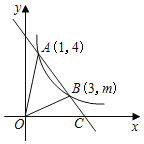
【题目】如图,直线y=k1x+b与双曲线y=![]() 交于点A(1,4),点B(3,m).
交于点A(1,4),点B(3,m).
(1)求k1与k2的值;
(2)求△AOB的面积.
【答案】(1)k1与k2的值分别为﹣![]() ,4;(2)
,4;(2)![]()
【解析】
(1)先把A点坐标代入y=![]() 中可求出k2得到反比例函数解析式为y=
中可求出k2得到反比例函数解析式为y=![]() ,再利用反比例函数解析式确定B(3,
,再利用反比例函数解析式确定B(3,![]() ),然后利用待定系数法求一次函数解析式得到k1的值;
),然后利用待定系数法求一次函数解析式得到k1的值;
(2)设直线AB与x轴交于C点,如图,利用x轴上点的坐标特征求出C点坐标,然后根据三角形面积公式,利用S△AOB=S△AOC﹣S△BOC计算.
解:(1)把A(1,4)代入y=![]() 得k2=1×4=4,
得k2=1×4=4,
∴反比例函数解析式为y=![]() ,
,
把B(3,m)代入y=![]() 得3m=4,解得m=
得3m=4,解得m=![]() ,则B(3,
,则B(3,![]() ),
),
把A(1,4),B(3,![]() )代入y=k1x+b得
)代入y=k1x+b得 ,解得
,解得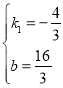 ,
,
∴一次函数解析式为y=﹣![]() x+
x+![]() ,
,
∴k1与k2的值分别为﹣![]() ,4;
,4;
(2)设直线AB与x轴交于C点,如图,
当y=0时,﹣![]() x+
x+![]() =0,解得x=4,则C(4,0),
=0,解得x=4,则C(4,0),
∴S△AOB=S△AOC﹣S△BOC=![]() ×4×4﹣
×4×4﹣![]() ×4×
×4×![]() =
=![]() .
.



 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
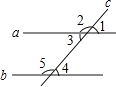
【题目】如图,直线a∥b,直线c与a、b都相交,从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于小岛M的北偏东45°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.
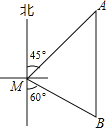
(1)求渔船从A到B的航行过程中与小岛M之间的最小距离(结果用根号表示):
(2)若渔船以20海里/小时的速度从B沿BM方向行驶,求渔船从B到达小岛M的航行时间(结果精确到0.1小时).(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且利润率不得高于![]() .经市场调查,每天的销售量
.经市场调查,每天的销售量![]() (千克)与每千克售价
(千克)与每千克售价![]() (元)满足一次函数关系,部分数据如下表:
(元)满足一次函数关系,部分数据如下表:
售价 | 45 | 50 | 55 |
销售量 | 110 | 100 | 90 |
(1)求![]() 与
与![]() 之间的函数表达式,并写出自变量的范围;
之间的函数表达式,并写出自变量的范围;
(2)设每天销售该商品的总利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数表达式(利润=收入-成本),并求出售价为多少元时每天销售该商品所获得最大利润,最大利润是多少?
之间的函数表达式(利润=收入-成本),并求出售价为多少元时每天销售该商品所获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为_____.
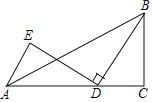
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )

A.2mB.4mC.![]() mD.
mD.![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
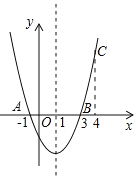
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示方向经过点B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t(单位:秒),他与教练的距离为y(单位:米),表示y与t的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的( )

A. 点M B. 点N C. 点P D. 点Q
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com