练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差：
    甲乙丙丁
    平均数（环）9.149.159.149.15
    方差6.66.86.76.6
    根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（　　）
    A．甲B．乙C．丙D．丁

    分析 利用平均数和方差的意义进行判断．

    解答 解：丁的平均数最大，方差最小，成绩最稳当，
    所以选丁运动员参加比赛．
    故选D．

    点评 本题考查了方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．抛物线y=4x2-2ax+b与x轴相交于A（x1，0），B（x2，0）（0＜x1＜x2）两点，与y轴交于点C．
    （1）设AB=2，tan∠ABC=4，求该抛物线的解析式；
    （2）在（1）中，若点D为直线BC下方抛物线上一动点，当△BCD的面积最大时，求点D的坐标；
    （3）是否存在整数a，b使得1＜x1＜2和1＜x2＜2同时成立，请证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．分解因式：ab-b2=b（a-b）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

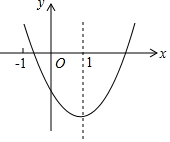    17．二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，下列结论：
    ①ab＜0；②b2＞4ac；③a+b+2c＜0；④3a+c＜0．
    其中正确的是（　　）
    A．①④B．②④C．①②③D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图1，抛物线y=ax2+bx+2与x轴交于A，B两点，与y轴交于点C，AB=4，矩形OBDC的边CD=1，延长DC交抛物线于点E．
    （1）求抛物线的解析式；
    （2）如图2，点P是直线EO上方抛物线上的一个动点，过点P作y轴的平行线交直线EO于点G，作PH⊥EO，垂足为H．设PH的长为l，点P的横坐标为m，求l与m的函数关系式（不必写出m的取值范围），并求出l的最大值；
    （3）如果点N是抛物线对称轴上的一点，抛物线上是否存在点M，使得以M，A，C，N为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

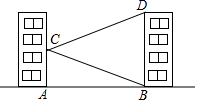    14．如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°，教学楼底部B的俯角为20°，量得实验楼与教学楼之间的距离AB=30m．
    （1）求∠BCD的度数．
    （2）求教学楼的高BD．（结果精确到0.1m，参考数据：tan20°≈0.36，tan18°≈0.32）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

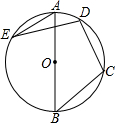    1．如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED=20°，则∠BCD的度数为（　　）
    A．100°B．110°C．115°D．120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如图，在菱形ABCD中，若AC=6，BD=8，则菱形ABCD的面积是24．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

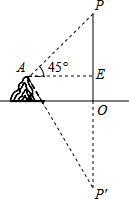    12．在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处，观察到飞艇底部标志P处的仰角为45°，又观其在湖中之像的俯角为60°，则飞艇底部P距离湖面的高度为（参考等式：$\frac{1}{\sqrt{3}-1}$=$\frac{\sqrt{3}+1}{2}$）（　　）
    A．25$\sqrt{3}$+75B．50$\sqrt{3}$+50C．75$\sqrt{3}$+75D．50$\sqrt{3}$+100

    查看答案和解析>>

    同步练习册答案