
 (1)计算:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1
(1)计算:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1分析 (1)根据零指数幂的定义、二次根式的乘法法则、负整数指数幂的定义计算,即可得出结果;
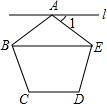
(2)首先根据多边形内角和计算公式计算出每一个内角的度数,再根据等腰三角形的性质计算出∠AEB,然后根据平行线的性质可得答案.
解答 (1)解:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1
=1-$\sqrt{16}$+3
=1-4+3
=0
(2)解:∵ABCDE是正五边形,
∴∠BAE=(5-2)×180°÷5=108°,AB=AE,
∴∠AEB=∠ABE=(180°-108°)÷2=36°,
∵l∥BE,
∴∠1=∠AEB=36°.
点评 此题考查了零指数幂的定义、二次根式的乘法法则、负整数指数幂的定义、正多边形的内角和定理,以及三角形内角和定理,平行线的性质;熟记有关定义和性质是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{k=2}\\{m=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{k=2}\\{m=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{k=3}\\{m=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{k=-3}\\{m=-2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com