
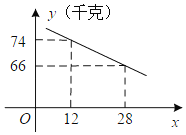
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式.
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实7000千克.
(3)当增种果树多少棵时,果园的总产量w(千克)最大?此时每棵果树的产量是多少?
【答案】(1)y=﹣![]() x+80;(2)增种果树20棵时,果园可以收获果实7000千克;(3)当增种果树40棵时,果园的总产量最大.每颗果树的产量为60千克.
x+80;(2)增种果树20棵时,果园可以收获果实7000千克;(3)当增种果树40棵时,果园的总产量最大.每颗果树的产量为60千克.
【解析】
(1)根据该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示即可求解;
(2)根据(1)中求得的函数关系式,代入7000千克,即可求解;
(3)确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义.
解:(1)根据题中的图可以看出,y与x为一次函数的关系,
设函数关系式为y=kx+b,将(12,74)、(28,66)代入关系式可得![]()
解得k=﹣![]() ,b=80,
,b=80,
所以y与x之间的函数关系式为y=﹣![]() x+80.
x+80.
(2)根据题意可列方程(-![]() x+80)(x+80)=7000,
x+80)(x+80)=7000,
化简得x2﹣80x+1200=0,解得x1=20,x2=60,
因为题中要求投入成本最低的情况下,所以x2=60不符题意舍去,
答:增种果树20棵时,果园可以收获果实7000千克.
(3)根据题意可列函数关系式w=(﹣![]() x+80)(x+80)=﹣
x+80)(x+80)=﹣![]() (x﹣40)2+7200.
(x﹣40)2+7200.
令y≥0,可求出自变量x的取值范围是0≤x≤160,
所以当x=40时,w可取到最大值7200,每颗果树的产量为y=﹣![]() x+80=60
x+80=60
答:当增种果树40棵时,果园的总产量最大.每颗果树的产量为60千克.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE.
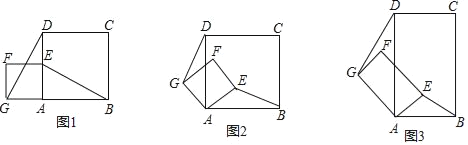
(1)发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是 ;②直线DG与直线BE之间的位置关系是 .
(2)探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.
(3)应用:在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,与x轴相交于点B.
,与x轴相交于点B.
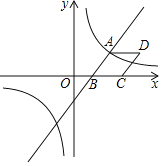
(1)求k的值;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数![]() 的图象,请直接写出:当
的图象,请直接写出:当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 以每秒3个单位长的速度运动至点
以每秒3个单位长的速度运动至点![]() ,过点
,过点![]() 作
作![]() 射线
射线![]() 于点
于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ).
).
(1)线段![]() 的长为 (用含
的长为 (用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 与
与![]() 的周长的比为
的周长的比为![]() 时,求
时,求![]() 的值.
的值.
(3)设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当直线![]() 把
把![]() 分成的两部分图形中有一个是轴对称图形时,直接写出
分成的两部分图形中有一个是轴对称图形时,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
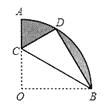
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
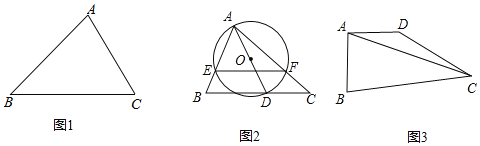
(1)如图1,在△ABC中,∠A=75°,∠C=60°,AC=6![]() ,求△ABC的外接圆半径R的值;
,求△ABC的外接圆半径R的值;
问题探究
(2)如图2,在△ABC中,∠BAC=60°,∠C=45°,AC=8![]() ,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
问题解决
(3)如图3,在四边形ABCD中,∠BAD=90°,∠BCD=30°,AB=AD,BC+CD=12![]() ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com