
【题目】如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.
(1)求b+c的值;
(2)若点C在抛物线上,且四边形OABC是平行四边形,求抛物线的解析式;
(3)在(2)条件下,点P(不与A,C重合)是抛物线上的一点,点M是y轴上一点,当△BPM是等腰直角三角形时,直接写出点M的坐标..

【答案】(1)1;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据抛物线![]() 与
与![]() 轴交于
轴交于![]() 点,求出
点,求出![]() 点的坐标,再根据
点的坐标,再根据![]() 求出
求出![]() 点的坐标,将
点的坐标,将![]() 点坐标代入解析式,整理后即可求出
点坐标代入解析式,整理后即可求出![]() 的值;
的值;
(2)若四边形OABC是平行四边形,则![]() 用
用![]() 表示出
表示出![]() 点的坐标,把
点的坐标,把![]() 点的坐标代入解析式,求出
点的坐标代入解析式,求出![]() 和
和![]() 的关系,结合(1)问,求出
的关系,结合(1)问,求出![]() 和
和![]() 的值,进而求出抛物线的解析式;
的值,进而求出抛物线的解析式;
(3)![]() 是等腰直角三角形,设点
是等腰直角三角形,设点![]() 的坐标为
的坐标为![]() 由
由![]() ,列出关于x的一元二次方程,求出
,列出关于x的一元二次方程,求出![]() 的值,即可求出
的值,即可求出![]() 的坐标.
的坐标.
试题解析:(1)∵抛物线![]() 与y轴正半轴交于B点,
与y轴正半轴交于B点,
∴点B的坐标为(0,c),
∵OA=OB,
∴点A的坐标为(c,0),将点A(c,0)代入![]() 得
得![]()
∵c≠0,整理得b+c=1;

(2)如图,如果四边形OABC是平行四边形,那么CO∥AB,BC∥AO,
∴点C的坐标可以表示为(c,c),
当点C(c,c)落在抛物线![]() 上时,得
上时,得![]()
整理得b=c,
结合(1)问c+b=1,得![]()
故此时抛物线的解析式为![]()
(3)△BPM是等腰直角三角形,设点P的坐标为![]() ,
,
由BM=PM,列方程![]() ,解得
,解得![]() 或x=0(舍去),
或x=0(舍去),
所以当![]() 时,
时, ![]()
点![]() 的坐标为(0,1),
的坐标为(0,1),
同理当BP=PM时,求出![]() 点的坐标为
点的坐标为![]()
综上点M的坐标为(0,1)或![]()


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿矩形的边由![]() 运动,设点P运动的路程为x,
运动,设点P运动的路程为x,![]() 的面积为y,把y看作x的函数,函数的图像如图2所示,则
的面积为y,把y看作x的函数,函数的图像如图2所示,则![]() 的面积为( )
的面积为( )

A. 10 B. 16 C. 18 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2-4ax+b交x轴正半轴于A,B两点,交y轴正半轴于C,且OB=OC=3.
(1)求抛物线的解析式;
(2)点D为抛物线的顶点,点G在直线BC上,若![]() ,直接写出点G的坐标;
,直接写出点G的坐标;
(3)将抛物线向上平移m个单位,交BC于点M,N(如图2),若∠MON=45°,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,若∠B=56°,∠C=42°,则∠DAE的度数为( )
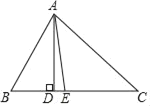
A. 3°B. 7°C. 11°D. 15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(![]() a2b)2(﹣9ab)÷(-
a2b)2(﹣9ab)÷(-![]() a3b2);
a3b2);
(2)(x+2y)(x﹣2y)﹣(x+y)(x﹣y);
(3)[(2a+b)2﹣(a﹣b)(3a﹣b)﹣a]÷(﹣![]() a),其中a=﹣1,b=
a),其中a=﹣1,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
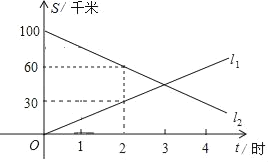
【题目】A,B两地相距100千米,甲,乙两人骑车同时分别从A、B两地相向而行,假设他们都保持匀速行驶,直线l1,l2分别表示甲,乙两人与A地的距离S(单位:km)与行驶时间t(单位:h)之间关系的图象.
根据图象提供的信息,解答下列问题:
(1)甲、乙两人的速度分别是多少?
(2)经过多长时间,两人相遇?
(3)分别写出甲,乙两人与A地的距离S(单位:km)与行驶时间t(单位:h)之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
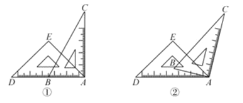
【题目】一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com