
分析 分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=CD-BD,分别计算出CD的长,再利用三角形的面积公式计算出面积.
解答 解:(1)如图1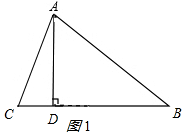 ,锐角△ABC中,AB=15,AC=13,BC边上高AD=12
,锐角△ABC中,AB=15,AC=13,BC边上高AD=12
在Rt△ACD中AB=13,AD=12,
由勾股定理得
CD2=AC2-AD2=132-122=25,
∴C=5,
在Rt△ABD中,AB=15,AD=12,
由勾股定理得
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC的长为BD+DC=9+5=14,
△ABC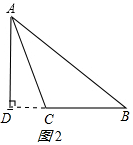 的面积:$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×14×12=84;
的面积:$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×14×12=84;
(2)钝角△ABC中,AB=15,AC=13,BC边上高AD=12
在Rt△ACD中,AC=13,AD=12,由勾股定理得
CD2=AC2-AD2=132-122=25,
∴CD=5,
在Rt△ABD中,AB=15,AD=12,由勾股定理得
BD2=AB2-AD2=152-122=81,
∴BD=9,
∴BC=DB-CD=9-5=4.
△ABC的面积:$\frac{1}{2}$×BC×AD=$\frac{1}{2}$×4×12=24;综上所述:△ABC的面积为84cm2或24cm2.
点评 本题考查了勾股定理,以及三角形的面积计算,把三角形斜边转化到直角三角形中用勾股定理解答.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |a|一定是正数 | B. | -a一定是负数 | ||
| C. | -(-a)一定是正数 | D. | 如果$\frac{|a|}{a}=-1$,那么a<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
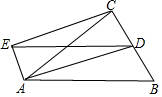 已知:如图,在△ABC中点D为BC边的中点,四边形ABDE为平行四边形.
已知:如图,在△ABC中点D为BC边的中点,四边形ABDE为平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
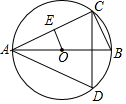 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com