
【题目】己知![]() 是
是![]() 的两条弦,
的两条弦,![]() .若
.若![]() 的直径为
的直径为![]() ,则弦
,则弦![]() 和
和![]() 之间的距离是__________.
之间的距离是__________.
【答案】1或7
【解析】
连接OA,OC,作直线EF⊥AB于E,交CD于F,由AB∥CD,根据垂径定理得到AE=![]() AB=4,CF=
AB=4,CF=![]() CD=3,再根据勾股定理可计算出OF=4,OE=3,然后分类讨论:当AB和CD在圆心的同侧时,则EF=OFOE;②当AB和CD在圆心的两侧时,则EF=OE+OF.
CD=3,再根据勾股定理可计算出OF=4,OE=3,然后分类讨论:当AB和CD在圆心的同侧时,则EF=OFOE;②当AB和CD在圆心的两侧时,则EF=OE+OF.
如图所示,连接OA,OC.作直线EF⊥AB于E,交CD于F,
∵AB∥CD,
∴EF⊥CD.
∵![]() 的直径为10,
的直径为10,
∴OA=OC=5

∵OE⊥AB,OF⊥CD,
∴AE=![]() AB=4,CF=
AB=4,CF=![]() CD=3,
CD=3,
∴OE=![]() =3, OF=
=3, OF=![]() =4
=4
①当AB和CD在圆心的同侧时,则EF=OFOE=1;
②当AB和CD在圆心的两侧时,则EF=OE+OF=7.
则AB与CD间的距离为1或7.
故答案为:1或7.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度.小正方形的顶点称为格点![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() .
.
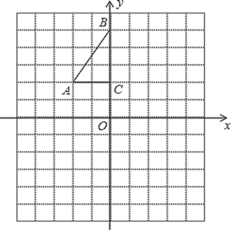
(1)将![]() 以点
以点![]() 为旋转中心旋转
为旋转中心旋转![]() ,得到
,得到![]() ,请画出的图形
,请画出的图形![]() ;
;
(2)平移![]() ,使点
,使点![]() 的对应点
的对应点![]() 坐标为
坐标为![]() ,请画出平移后对应的
,请画出平移后对应的![]() ;
;
(3)若将![]() 绕某一点旋转可得到
绕某一点旋转可得到![]() ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(4)请画出一个以![]() 为对角线,面积是20的菱形
为对角线,面积是20的菱形![]() (要求
(要求![]() ,
,![]() 是格点).
是格点).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式是![]() .
.
(1)用配方法将![]() 化成
化成![]() 的形式,并写出该二次函数的对称轴和顶点坐标;
的形式,并写出该二次函数的对称轴和顶点坐标;
(2)二次函数![]() 的图象与x轴相交吗?说明理由;若相交,求出交点坐标.
的图象与x轴相交吗?说明理由;若相交,求出交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣2,﹣![]() ,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn.
(1)请用列表或画树状图的方法表示取出数字的所有结果;
(2)求正比例函数y=kx的图象经过第一、三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,某校初三数学老师带领学生去测河宽,如图所示,某学生在河东岸点![]() 处观测到河对岸水边有一点
处观测到河对岸水边有一点![]() ,测得
,测得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,沿河岸向北前行20米到达
的方向上,沿河岸向北前行20米到达![]() 处,测得
处,测得![]() 在
在![]() 北偏西
北偏西![]() 的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈
的方向上,请你根据以上数据,帮助该同学计算出这条河的宽度.(参考数值:tan31°≈![]() ,sin31°≈
,sin31°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度向终点
的速度向终点![]() 匀速运动,点
匀速运动,点![]() 以
以![]() 的速度向终点
的速度向终点![]() 匀速运动,当有一点到达终点时,另一点也停止运动.设运动时间为
匀速运动,当有一点到达终点时,另一点也停止运动.设运动时间为![]() .
.

(1)当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(2)当![]() 为何值时,
为何值时,![]() 为
为![]() ?
?
(3)当![]() 为何值时,以点
为何值时,以点![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形?
为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
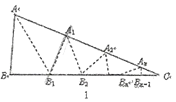
如图1,![]() 中,沿
中,沿![]() 的平分线
的平分线![]() 折叠,剪掉重叠部分;将余下部分沿
折叠,剪掉重叠部分;将余下部分沿![]() 的平分线
的平分线![]() 折叠,剪掉重叠部分;……;将余下部分沿
折叠,剪掉重叠部分;……;将余下部分沿![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合,无论折叠多少次,只要最后一次恰好重合,我们就称
重合,无论折叠多少次,只要最后一次恰好重合,我们就称![]() 是
是![]() 的好角.
的好角.
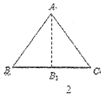
情形一:如图2,沿等腰三角形![]() 顶角
顶角![]() 的平分线
的平分线![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合;
重合;
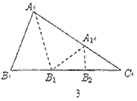
情形二:如图3,沿![]() 的
的![]() 的平分线
的平分线![]() 折叠,剪掉重叠部分;将余下的部分沿
折叠,剪掉重叠部分;将余下的部分沿![]() 的平分线
的平分线![]() 折叠,此时点
折叠,此时点![]() 与点
与点![]() 重合.
重合.
探究发现
(1)![]() 中,
中,![]() ,经过两次折叠,问
,经过两次折叠,问![]()
![]() 的好角(填写“是”或“不是”);
的好角(填写“是”或“不是”);
(2)若经过三次折叠发现![]() 是
是![]() 的好角,请探究
的好角,请探究![]() 与
与![]() (假设
(假设![]() )之间的等量关系 ;
)之间的等量关系 ;
根据以上内容猜想:若经过![]() 次折叠
次折叠![]() 是
是![]() 的好角,则
的好角,则![]() 与
与![]() (假设
(假设![]() )之间的等量关系为 ;
)之间的等量关系为 ;
应用提升:
(3)小丽找到一个三角形,三个角分别为![]() ,
,![]() ,
,![]() ,发现 是此三角形的好角;
,发现 是此三角形的好角;
(4)如果一个三角形的最小角是![]() ,且满足该三角形的三个角均是此三角形的好角;
,且满足该三角形的三个角均是此三角形的好角;
则此三角形另外两个角的度数 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.
(1)求甲、乙两种品牌的足球的单价各是多少元?
(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com