
����������ֱ��������2��1����3����4�IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ�����ſ�Ƭ���������ȡһ�Ų��Żأ����ÿ�Ƭ�ϵ����ּ�Ϊm�����������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊn��
��1���뻭����״ͼ��д����m��n�����п��ܵĽ����
��2������ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڶ������������ĸ��ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����������ABCD�У��Խ���BD�ij�Ϊ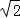 ������BD�Ƶ�B��ת��D����BC�ӳ����ϵĵ�D�䴦����D������·��Ϊ
������BD�Ƶ�B��ת��D����BC�ӳ����ϵĵ�D�䴦����D������·��Ϊ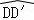 ����ͼ����Ӱ���ֵ�����ǣ�������
����ͼ����Ӱ���ֵ�����ǣ�������

| �� | A�� |
| B�� |
| C�� |
| D�� | ��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪������y=ax2+x+c��a��0������A����1��0����B��2��0�����㣬��y���ཻ�ڵ�C���������ߵĶ���Ϊ��M���Գ�����BC�ཻ�ڵ�N����x�ύ�ڵ�D��
��1����������ߵĽ���ʽ����M�����ꣻ
��2������ON��AC��֤������NOB=��ACB��
��3����E�Ǹ���������һ���㣬��λ�ڵ�һ���ޣ�����E��ֱ��BC�ľ���Ϊ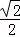 ʱ�����E�����ꣻ
ʱ�����E�����ꣻ
��4�������㣨3���������£�����EN�����ӳ�EN��y���ڵ�F��E��F�������ֱ��BC�Գ�����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�����龳����ͼ1��ֱ�����ǰ�ABC�У���C��90�㣬AC��BC����һ�����㹻���ĵ�ϸ��˿������ֱ�ǵĶ���D����ֱ�����ǰ�ABC��б��AB�ϣ��ٽ���ֱ���Ƶ�D��ת����ʹ�����߷ֱ������ǰ��AC�ߡ�BC�߽���P��Q���㡣
����̽������1������ת�����У�
����ͼ2����AD��BDʱ���߶�DP��DQ�к�������ϵ����˵�����ɡ�
����ͼ3����AD��2BDʱ���߶�DP��DQ�к�������ϵ����˵�����ɡ�
�۸�����Ԣ١��ڵ�̽���������д����AD��nBDʱ��DP��DQ�����������ϵΪ_______________��ֱ��д�����ۣ�����֤����
��2����AD��BDʱ����AB��20������PQ�����DPQ�����ΪS������ת�����У�S�Ƿ������Сֵ�����ֵ�������ڣ������Сֵ�����ֵ���������ڣ���˵�����ɡ�

ͼ1 ͼ2 ͼ3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
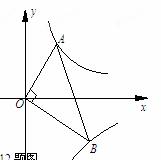
��֪��A��B�ֱ��ڷ��������� ��x��0����
��x��0����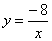 ��x��0����ͼ��
��x��0����ͼ��
�ϣ���OA��OB����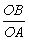 ��ֵΪ��������
��ֵΪ��������
A��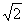 B��2 C��
B��2 C��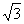 D��3
D��3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com