练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
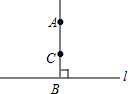
    2．如图所示，因为AB⊥l，BC⊥l，B为垂足，所以AB和BC重合，其理由是（　　）
    A．两点确定一条直线
    B．在同一平面内，过一点有且只有一条直线与已知直线垂直
    C．过一点能作一条垂线
    D．垂线段最短

    分析 直接利用直线的性质进而分析得出答案．

    解答 解：A、因为AB⊥l，BC⊥l，B为垂足，所以AB和BC重合，其理由是：
    在同一平面内，过一点有且只有一条直线与已知直线垂直．
    故选：B．

    点评 此题主要考查了直线的性质，正确把握直线的性质是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如图，在?ABCD中，E是BC上的一点，且AB=BE，AE、DC的延长线相交于点F，∠F=62°，求∠D的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列事件中，必然事件是（　　）
    A．a是实数，|a|≥0
    B．掷一枚硬币，正面朝上
    C．某运动员跳高的最好成绩是20.1m
    D．从车间刚生产的产品中任意抽取一个，是次品

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图1，一条细绳系着一个小球在平面内摆动，已知细绳从悬挂点O到球心的长度为50厘米，小球在带你B位置时达到最低点，当小球在左侧点A时与最低点B时细绳相应所成的角度∠AOB=37°．（取sin37°=0.6，cos37°=0.8，tan37°=0.75）
    （1）求点A与点B的高度差BC的值．
    （2）如图2，若在点O的正下方有一个阻碍物P，当小球从左往右落到最低处后，运动轨迹改变，变为以P为圆心，PB为半径继续向右摆动，当摆动至与点A在同一水平高度的点D时，满足PD部分细绳与水平线的夹角∠DPQ=30°，求OP的长度．

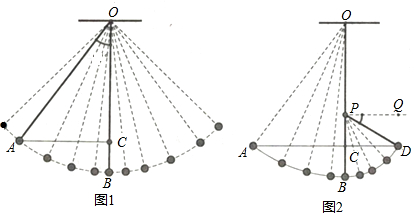
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．已知$\frac{1}{x}$-$\frac{1}{y}$=3，则代数式$\frac{2x-8xy-2y}{x-2xy-y}$的值为$\frac{14}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．在生活中，正方形总给我们美的享受，它在生活中的问题也很多，下面请同学们在美的视觉中研究问题：在正方形ABCD中，动点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动．
    （1）如图①，当点E自D向C，点F自C向B移动时，连接AE和DF交于点P，请你写出AE与DF的关系，并说明理由．
    （2）如图②，当点E，F分别移动到边DC，CB的延长线上时，连接AE和DF，（1）中的结论还成立吗？（请你直接作答，不需证明）
    （3）如图③，当点E自C向D，点F自B向C，分别在边CD，BC的延长线上移动时，连接AE和DF，（1）中的结论还成立吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．能确定四边形是平行四边形的条件的是（　　）
    A．一组对边平行，另一组对边相等B．一组对边平行，一组邻角相等
    C．一组对边平行且相等D．两条对角线相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．图1是一种可折叠台灯，它放置在水平桌面上，将其抽象成图2，其中点B，E，D均为可转动点．现测得AB=BE=ED=CD=15cm，经多次调试发现当点B，E所在直线垂直经过CD的中点F时（如图3所示）放置较平稳．
    （1）求平稳放置时灯座DC与灯杆DE的夹角的大小；
    （2）为保护视力，写字时眼睛离桌面的距离应保持在30cm，为防止台灯刺眼，点A离桌面的距离应不超过30cm，求台灯平稳放置时∠ABE的最大值．（结果精确到0.01°，参考数据：$\sqrt{3}$≈1.732，sin7.70°≈0.134，cos82.30°≈0.134，可使用科学计算器）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．某校数学兴趣小组在探究如何求tan 15°，cos15°的值，经过自主思考、合作交流讨论，得到以下思路：
    思路一　 如图1，在Rt△ABC中，∠C=90°，∠ABC=30°，延长CB至点D，使BD=BA，连接AD．设AC=1，则BD=BA=2，BC=$\sqrt{3}$．
    tanD=tan15°=$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{（2+\sqrt{3}）（2-\sqrt{3}）}$=2-$\sqrt{3}$．
    思路二　 利用科普书上的有关公式：
    tan（α±β）=$\frac{tanα+tanβ}{1±tanα•tanβ}$；
    cos（α±β）=cosαcosβ±sinαsinβ．
    例如α=60°，β=45°代入差角正切公式：
    tan15°=tan（60°-45°）=$\frac{tan60°-tan45°}{1+tan60°•tan45°}$=$\frac{\sqrt{3}-1}{1+\sqrt{3}}$=2-$\sqrt{3}$．
    思路三　 在顶角为30°的等腰三角形中，作腰上的高也可以…
    思路四　 …
    请解决下列问题（上述思路仅供参考）．
    （1）类比：求出tan75°的值和cos15°的值；
    （2）应用：如图2，某县要在宽为10米的幸福大道两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成105°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，求路灯的灯柱BC高度．
    （精确到0.1米，参考数据$\sqrt{6}$≈2.449，$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）

    查看答案和解析>>

    同步练习册答案