
【题目】已知:![]() ,OB、OC、OM、ON是
,OB、OC、OM、ON是![]() 内的射线.
内的射线.
![]() 如图1,若OM平分
如图1,若OM平分![]() ,ON平分
,ON平分![]() 当OB绕点O在
当OB绕点O在![]() 内旋转时,则
内旋转时,则![]() 的大小为______;
的大小为______;
![]() 如图2,若
如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() 当
当![]() 绕点O在
绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小;
的大小;
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,当
,当![]() 在
在![]() 内绕着点O以
内绕着点O以![]() 秒的速度逆时针旋转t秒时,
秒的速度逆时针旋转t秒时,![]() 和
和![]() 中的一个角的度数恰好是另一个角的度数的两倍,求t的值
中的一个角的度数恰好是另一个角的度数的两倍,求t的值

【答案】(1)78°;(2)∠MON=66°;(3)当t=3或t=33时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍.
【解析】
(1)由角平分线的定义可得∠BOM![]() ∠AOB,∠BON
∠AOB,∠BON![]() ∠BON,即可求∠MON的大小;
∠BON,即可求∠MON的大小;
(2)由角平分线的定义可得∠COM![]() ∠AOC,∠BON
∠AOC,∠BON![]() ∠BOD,即可求∠MON的大小;
∠BOD,即可求∠MON的大小;
(3)由题意可得∠AOC=54°+2t,∠AOM=27+t,∠BOD=126﹣2t,∠DON=63﹣t,分∠AOM=2∠DON,∠DON=2∠AOM两种情况讨论,列出方程可求t的值.
(1)∵OM平分∠AOB,ON平分∠BOD,∴∠BOM![]() ∠AOB,∠BON
∠AOB,∠BON![]() ∠BON.
∠BON.
∵∠MON=∠BOM+∠BON![]() ∠AOD,∴∠MON=78°.
∠AOD,∴∠MON=78°.
故答案为:78°.
(2)∵OM平分∠AOC,ON平分∠BOD,∴∠COM![]() ∠AOC,∠BON
∠AOC,∠BON![]() ∠BOD,∴∠MON=∠BON+∠COM﹣∠BOC
∠BOD,∴∠MON=∠BON+∠COM﹣∠BOC![]() ∠AOC
∠AOC![]() ∠BOD﹣24°
∠BOD﹣24°![]() (∠AOC+∠BOD)﹣24°,∴∠MON
(∠AOC+∠BOD)﹣24°,∴∠MON![]() (∠AOD+∠BOC)﹣24°
(∠AOD+∠BOC)﹣24°![]() 180°﹣24°=66°.
180°﹣24°=66°.
(3)∵∠BOC在∠AOD内绕着点O以2°/秒的速度逆时针旋转t秒,OM平分∠AOC,ON平分∠BOD,∴∠AOC=54°+2t,∠AOM=27+t,∠BOD=126﹣2t,∠DON=63﹣t.
若∠AOM=2∠DON时,即27+t=2(63﹣t),∴t=33;
若2∠AOM=∠DON,即2(27+t)=63﹣t,∴t=3.
综上所述:当t=3或t=33时,∠AOM和∠DON中的一个角的度数恰好是另一个角的度数的两倍.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=63°,∠ECB=117°.
(1) AB与ED平行吗?为什么?
(2)若∠P=∠Q,则∠1与∠2是否相等?说说你的理由.
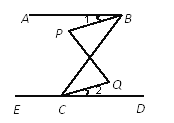
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于不等式组 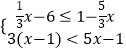 ,下列说法正确的是( )
,下列说法正确的是( )
A.此不等式组的正整数解为1,2,3
B.此不等式组的解集为﹣1<x≤ ![]()
C.此不等式组有5个整数解
D.此不等式组无解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄冈农科院培育的“黄金8号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.
(Ⅰ)根据题意,填写下表:
购买种子的数量/kg 1.5 2 3.5 4 …
付款金额/元 7.5 16 …
(Ⅱ)设购买种子数量为xkg,付款金额为y元,求y关于x的函数解析式;
(Ⅲ)若小明帮奶奶一次购买该种子花费了30元,求他购买种子的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题:
(1)x取何值时,代数式3x+2的值不大于代数式4x+3的值?
(2)当m为何值时,关于x的方程![]() x-1=m的解不小于3?
x-1=m的解不小于3?
(3)已知不等式2(x+3)-4<0, 化简:︳4x+1︱-︱2-4x︱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
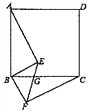
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程x2﹣(2k﹣1)x+k2﹣2k+3=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程的两个实数根分别为x1、x2 , 存不存在这样的实数k,使得|x1|﹣|x2|= ![]() ?若存在,求出这样的k值;若不存在,说明理由.
?若存在,求出这样的k值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程kx2+(2k+1)x+2=0.
(1)求证:无论k取任何实数时,方程总有实数根;
(2)当抛物线y=kx2+(2k+1)x+2图象与x轴两个交点的横坐标均为整数,且k为正整数时,若P(a,y1),Q(1,y2)是此抛物线上的两点,且y1>y2 , 请结合函数图象确定实数a的取值范围;
(3)已知抛物线y=kx2+(2k+1)x+2恒过定点,求出定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从4这点开始跳,则经2015次跳后它停在数对应的点上.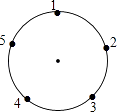
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com