
分析 根据题意画出图形,连接OG,OA,OB,根据正六边形的性质得出∠AOG=30°,再由锐角三角函数的定义得出AG的长,故可得出AB的长,由此可得出结论.
解答 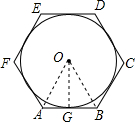 解:如图所示,连接OG,OA,OB,
解:如图所示,连接OG,OA,OB,
∵正六边形ABCDEF外切于⊙O,
∴∠AOG=30°.
∵OG=r,
∴AG=OG•tan30°=$\frac{\sqrt{3}}{3}$r,
∴AB=$\frac{2\sqrt{3}}{3}$r,
∴该正六边形的周长=$4\sqrt{3}$r,S正六边形ABCDEF=6S△AOB=2$\sqrt{3}$r2.
答:该正六边形的周长和面积分别是$4\sqrt{3}$r,2$\sqrt{3}$r2.
点评 本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
 如图所示是某工厂的大门,它是由一个正方形和一个半圆组成的,正方形的边长为5米,一辆装货的卡车宽为4米,高为6米,则这辆卡车能否通过此大门?说明理由.
如图所示是某工厂的大门,它是由一个正方形和一个半圆组成的,正方形的边长为5米,一辆装货的卡车宽为4米,高为6米,则这辆卡车能否通过此大门?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
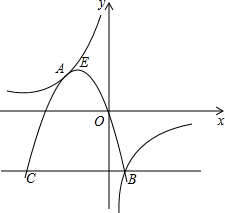 如图,抛物线y=ax2+bx+c(a<0)与双曲线相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
如图,抛物线y=ax2+bx+c(a<0)与双曲线相交于点A,B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
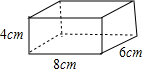 如图所示的是一个长8cm,宽6cm,高4cm的长方体,现在把它等分为24个棱长为2cm的小正方体
如图所示的是一个长8cm,宽6cm,高4cm的长方体,现在把它等分为24个棱长为2cm的小正方体查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{-5}$ | D. | $\sqrt{(-5)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
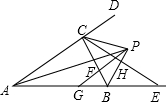 如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:
如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com