
【题目】如图![]() ,已知在四边形
,已知在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() .
.

![]() 求证:四边形
求证:四边形![]() 是菱形;
是菱形;
![]() 若
若![]() ,如图
,如图![]() 所示:
所示:
①求证:![]() ;
;
②若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)证明见解析(2)见解析
【解析】
(1)根据平行四边形的性质得出AD∥BC,求出四边形ABFE是平行四边形,求出AB=AE,根据菱形的判定得出即可;
(2)①过O作ON∥BC交DC于N,根据矩形的判定得出四边形ABCD是矩形,根据矩形的性质得出∠ADC=∠BCD=90°,AD∥BC,求出N为DC的中点,ON⊥DC,根据线段垂直平分线性质得出OD=OC,即可得出答案;
②根据正方形的判定得出四边形ABFE是正方形,根据正方形的性质得出∠AEB=45°,根据三角形外角性质求出∠EDO=30°,求出∠ODC即可.
![]() 证明:∵四边形
证明:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴平行四边形![]() 是菱形;
是菱形;
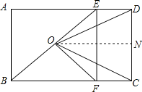
![]() ①过
①过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() 为
为![]() 的中点,
的中点,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
②解:∵四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图①,直角三角形ABC中,∠B=90°.将它放在平面直角坐标系中,A(0,1),且满足(AB-4)2+![]() =0.
=0.
(1)求直线AC的解析式.
(2)在直线BC上是否存在点P,使S△APC= 6?若存在,求P点坐标;若不存在,说明理由.
(3)如果M在y轴上,且△AMC是以AC为腰的等腰三角形,求M的坐标
(4)如果D是AC的中点,问在y轴上是否存在点M,使得MD+ ![]() AC最小?存在的话,请直接写出M的坐标。
AC最小?存在的话,请直接写出M的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝网店销售台灯,成本为每个![]() 元.销售大数据分析表明:当每个台灯售价为
元.销售大数据分析表明:当每个台灯售价为![]() 元时,平均每月售出
元时,平均每月售出![]() 个;若售价每上涨
个;若售价每上涨![]() 元,其月销售量就减少
元,其月销售量就减少![]() 个,若售价每下降
个,若售价每下降![]() 元,其月销售量就增加
元,其月销售量就增加![]() 个.
个.
![]() 若售价上涨
若售价上涨![]() 元
元![]() ,每月能售出________个台灯.
,每月能售出________个台灯.
![]() 为迎接“双十一”,该网店决定降价促销,在库存为
为迎接“双十一”,该网店决定降价促销,在库存为![]() 个台灯的情况下,若预计月获利恰好为
个台灯的情况下,若预计月获利恰好为![]() 元,求每个台灯的售价.
元,求每个台灯的售价.
![]() 在库存为
在库存为![]() 个台灯的情况下,若预计月获利恰好为
个台灯的情况下,若预计月获利恰好为![]() 元,直接写出每个台灯的售价.
元,直接写出每个台灯的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=6,AB=10,则DE的长为______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用围棋子摆出的图案(用棋子的位置用用有序数对表示,如![]() 点在
点在![]() ),如果再摆一黑一白两枚棋子,使
),如果再摆一黑一白两枚棋子,使![]() 枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )

A. 黑(3,3),白(3,1) B. 黑(3,1),白(3,3)
C. 黑(1,5),白(5,5) D. 黑(3,2),白(3,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A. 点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动_________秒后,△AMN是等边三角形?
(2)点M、N在BC边上运动时,运动_______秒后得到以MN为底边的等腰三角形△AMN?
(3)M、N同时运动几秒后,△AMN是直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B 两点分别位于一个池塘的两端,小明想用绳子测量A、B 间的距离,但绳子不够长,请你利用三角形全等的相关知识帮他设计一种方案测量出A、B间的距离,写出具体的方案,并解释其中的道理,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com