
【题目】如图1,已知∠ACD是△ABC的一个外角,我们容易证明∠ACD=∠A+∠B,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
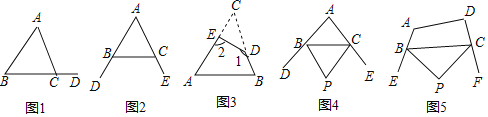
尝试探究:(1)如图2,∠DBC与∠ECB分别为△ABC的两个外角,则∠DBC+∠ECB ∠A+180°(横线上填>、<或=)
初步应用:(2)如图3,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=135°,则∠2-∠C= .
解决问题:(3)如图4,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
(4)如图5,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,请利用上面的结论探究∠P与∠A、∠D的数量关系.
【答案】(1)=;(2)45°;(3)∠P=90°-![]() ∠A;(4)∠P=180°-
∠A;(4)∠P=180°-![]() ∠A-
∠A-![]() ∠D
∠D
【解析】
(1)根据三角形外角的性质可得∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,然后求和并根据三角形的内角和定理即可得出结论;
(2)根据(1)的结论即可求出∠2-∠C;
(3)根据(1)的结论可得∠DBC+∠ECB=∠A+180°,然后根据角平分线的定义计算出∠CBP+∠BCP,再根据三角形的内角和定理即可得出结论;
(4)根据四边形的内角和可得∠ABC+∠DCB=360°-∠A-∠D,然后根据平角的定义可推出∠EBC+∠FCB=∠A+∠D,然后根据角平分线的定义和三角形的内角和定理即可得出结论.
解:(1)∵∠DBC与∠ECB分别为△ABC的两个外角
∴∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC
∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC=∠A+(∠ACB+∠A+∠ABC)=∠A+180°
故答案为:=;
(2)由(1)的结论可知:∠1+∠2=∠C+180°
∵∠1=135°
∴∠2-∠C=180°-∠1=45°
故答案为:45°
(3)由(1)的结论可知:∠DBC+∠ECB=∠A+180°
∵BP、CP分别平分外角∠DBC、∠ECB,
∴∠CBP=![]() ∠DBC,∠BCP=
∠DBC,∠BCP=![]() ∠ECB
∠ECB
∴∠CBP+∠BCP
=![]() ∠DBC+
∠DBC+![]() ∠ECB
∠ECB
=![]() (∠DBC+∠ECB)
(∠DBC+∠ECB)
=![]() (∠A+180°)
(∠A+180°)
=![]() ∠A+90°
∠A+90°
∵∠CBP+∠BCP+∠P=180°
∴∠P=180°-(∠CBP+∠BCP)
=180°-(![]() ∠A+90°)
∠A+90°)
=90°-![]() ∠A
∠A
故答案为:∠P=90°-![]() ∠A
∠A
(4)根据四边形的内角和可得∠ABC+∠DCB=360°-∠A-∠D
∵∠EBC=180°-∠ABC,∠FCB=180°-∠DCB
∴∠EBC+∠FCB
=180°-∠ABC+180°-∠DCB
=360°-(∠ABC+∠DCB)
=360°-(360°-∠A-∠D)
=∠A+∠D
∵BP、CP分别平分外角∠EBC、∠FCB,
∴∠CBP=![]() ∠EBC,∠BCP=
∠EBC,∠BCP=![]() ∠FCB
∠FCB
∴∠CBP+∠BCP
=![]() ∠EBC+
∠EBC+![]() ∠FCB
∠FCB
=![]() (∠EBC+∠FCB)
(∠EBC+∠FCB)
=![]() (∠A+∠D)
(∠A+∠D)
∵∠CBP+∠BCP+∠P=180°
∴∠P=180°-(∠CBP+∠BCP)
=180°-![]() (∠A+∠D)
(∠A+∠D)
=180°-![]() ∠A-
∠A-![]() ∠D
∠D


科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有:a+b![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;
(2)利用所探索的结论,用完全平方式表示出:7+4![]() = .
= .
(3)请化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,七(1)班的小明等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话,试根据对话中的信息,解答下列问题:
儿子:爸爸,成人门票是每张20元;学生门票是五折优惠;
团体票(16人及16人以上),按成人票的六折优惠.
爸爸:我们成人、学生一共12人,共需200元.
(1)设小明他们一共去了学生![]() 人,则成人购买门票的总费用为: 元;(用含
人,则成人购买门票的总费用为: 元;(用含![]() 的代数式表示)
的代数式表示)
(2)七(1)班小明他们一共去了几个成人、几个学生?
(3)正在购票时,小明发现七(2)班的小军等10名同学和他们的7名家长共17人也来购票,他们准备联合一起购买门票,请你为这29人的团队设计出最省的购票方案(直接写出方案即可,无需讨论),并求出此时的购票费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某学校决定开设民族器乐选修课.为了更贴合学生的兴趣,对学生最喜爱的一种民族乐器进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
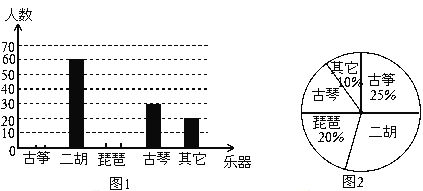
(1)在这次抽样调查中,共调查 名学生;
(2)请把条形图(图1)补充完整;
(3)求扇形统计图(图2)中,二胡部分所对应的圆心角的度数;
(4)如果该校共有学生1500名,请你估计最喜爱古琴的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现
如图1,在边长为1的正方形网格中,连接格点![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中![]() 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点
不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点![]() 、
、![]() ,可得
,可得![]() ,则
,则![]() ,连接
,连接![]() ,那么
,那么![]() 就变换到中
就变换到中![]() .
.
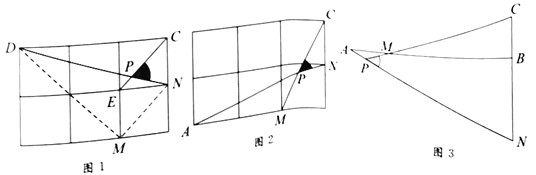
问题解决
(1)直接写出图1中![]() 的值为_________;
的值为_________;
(2)如图2,在边长为1的正方形网格中,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值;
的值;
思维拓展
(3)如图3,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,用上述方法构造网格求
,用上述方法构造网格求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() ,连接
,连接![]() ,
,![]() ,
,![]() .在此运动过程中,下列结论:①
.在此运动过程中,下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积保持不变;④当
的面积保持不变;④当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
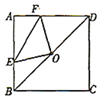
A.①②B.②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义![]() 为一次函数
为一次函数![]() 的特征数.
的特征数.
(1)若特征数是![]() 的一次函数为正比例函数,求
的一次函数为正比例函数,求![]() 的值;
的值;
(2)设点![]() 分别为抛物线y=(3x+2m)(x-4)
分别为抛物线y=(3x+2m)(x-4)![]() 与
与![]() 轴的交点,其中
轴的交点,其中![]() ,且
,且![]() 的面积为4,
的面积为4,![]() 为原点,求图象过
为原点,求图象过![]() 两点的一次函数的特征数.
两点的一次函数的特征数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
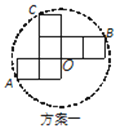
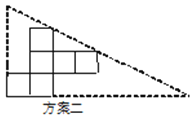
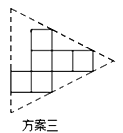
说明:方案一图形中的圆过点A,B,C,圆心O也是正方形的顶点;
回答问题(直接写出结果):
(1)方案二中,直角三角形纸片的两条直角边长分别为_______cm和_______cm;
(2)小明通过计算,发现方案一中纸片的利用率是________(填准确值),近似值约为38.2%.相比之下,方案二的利用率是________%.小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com