
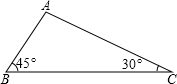
 如图所示,△ABC中,∠A=30°,∠B=45°,AC=2,求AB及△ABC的面积.
如图所示,△ABC中,∠A=30°,∠B=45°,AC=2,求AB及△ABC的面积.| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| ||
| 2 |


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
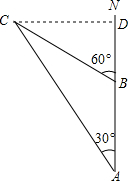 如图所示,一艘货船以30 km/h的速度向正北航行,在A出看见灯塔C在船的北偏西30°,20s后货船航行至B处,看见灯塔C在船的北偏西60°,若货船向北继续航行,当灯塔C在船的正西方向时,灯塔与货船相距多少米(精确到0.1m)?
如图所示,一艘货船以30 km/h的速度向正北航行,在A出看见灯塔C在船的北偏西30°,20s后货船航行至B处,看见灯塔C在船的北偏西60°,若货船向北继续航行,当灯塔C在船的正西方向时,灯塔与货船相距多少米(精确到0.1m)?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
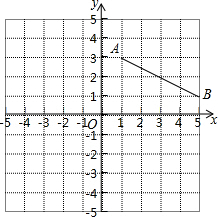 如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为( )
如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为( )A、
| ||
| B、15 | ||
| C、3 | ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
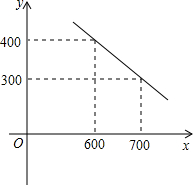 某公司试销一种成本单价为500元/间的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系.
某公司试销一种成本单价为500元/间的新产品,规定试销时的销售单价不低于成本单价,又不高于800元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com