已知抛物线y=x2+bx+c经过原点,且在x轴的正半轴上截得的线段长为4,对称轴为直线x=m.过点A的直线绕点A ( m,0 ) 旋转,交抛物线于点B ( x,y ),交y轴负半轴于点C,过点C且平行于x轴的直线与直线x=m交于点D,设△AOB的面积为S1,△ABD的面积为S2.
(1)求这条抛物线的顶点的坐标;
(2)判断S1与S2的大小关系,并证明你的结论.
分析:(1)根据抛物线经过原点,且在x轴的正半轴上截得的线段的长为4,得出c=0,图象与x轴的交点A、E的坐标,对称轴为直线x=2,代入即可求出答案;
(2)设经过点A(2,0)的直线为y=kx+b(k≠0),代入求出y=-
x+b.设点B
1的坐标为(x
1,-
x+b),点B
2的坐标为(x
2,-
x+b).当交点为B
1时,根据三角形的面积公式求出即可;当交点为B
2时,根据三角形的面积公式求出即可.
解答: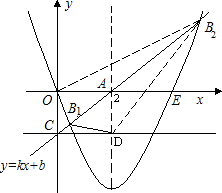
解:(1)∵抛物线y=x
2+bx+c经过原点,且在x轴的正半轴上截得的线段的长为4,
∴c=0,A(2,0),图象与x轴的另一个交点E的坐标为(4,0),对称轴为直线x=2.
∴抛物线为y=x
2+bx经过点E(4,0).
∴b=-4,∴y=x
2-4x.
∴顶点坐标为(2,-4).
答:这条抛物线的顶点的坐标是(2,-4).
(2)答:S
1与S
2的大小关系是S
1=S
2.
证明:设经过点A(2,0)的直线为y=kx+b(k≠0),
∴0=2k+b.∴k=-
b,
∴y=-
x+b,
∴点B
1的坐标为(x
1,-
x+b),
点B
2的坐标为(x
2,-
x+b),
当交点为B
1时,
S
1=
×2×|-
x
1+b|=b-
x
1,
S
2=
×|b|×|2-x
1|=b-
x
1,
∴S
1=S
2,
当交点为B
2时,
S
1=
×2×|-
x
2+b|=-
x
2+b,
S
2=
×|b|×|x
2-2|=-
x
2+b,
∴S
1=S
2,
综上所述,S
1=S
2.
点评:本题主要考查对三角形的面积,二次函数图象上点的坐标特征等知识点的理解和掌握,能熟练地运用性质进行计算是解此题的关键.

 解:(1)∵抛物线y=x2+bx+c经过原点,且在x轴的正半轴上截得的线段的长为4,
解:(1)∵抛物线y=x2+bx+c经过原点,且在x轴的正半轴上截得的线段的长为4,

 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.