
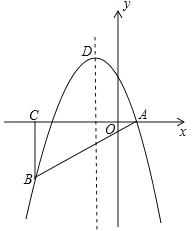
【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线![]() 经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.
经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.
(1)求抛物线的解析式;
(2)点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)点E的坐标为(﹣
;(2)点E的坐标为(﹣![]() ,﹣
,﹣![]() );(3)点P的坐标为(﹣
);(3)点P的坐标为(﹣![]() ,
,![]() )或(﹣1﹣
)或(﹣1﹣![]() ,﹣
,﹣![]() )或(﹣1+
)或(﹣1+![]() ,﹣
,﹣![]() ).
).
【解析】
试题(1)首先依据等腰直角三角形的性质求得点B的坐标,然后将点A和点B的坐标代入抛物线的解析式求解即可;
(2)设直线AB的解析式为y=kx+b,将点A和点B的坐标代入可求得直线AB的解析式,设点E的坐标为(t,t﹣1),则点F的坐标为(t,![]() ),然后列出EF关于t的函数关系式,最后利用配方法求得EF的最大值即可;
),然后列出EF关于t的函数关系式,最后利用配方法求得EF的最大值即可;
(3)过点F作直线a⊥EF,交抛物线与点P,过点E作直线b⊥EF,交抛物线P′、P″,先求得点E和点F的纵坐标,然后将点E和点F的纵坐标代入抛物线的解析式求得对应的x的值,从而可求得点P、P′、P″的坐标.
试题解析:(1)∵A,C的坐标分别为(1,0),(﹣4,0),∴AC=5.∵△ABC为等腰直角三角形,∠C=90°,∴BC=AC=5,∴B(﹣4,﹣5).将点A和点B的坐标代入得:![]() ,解得:
,解得:![]() ,∴抛物线的解析式为
,∴抛物线的解析式为![]() .
.
(2)如图1所示:

设直线AB的解析式为y=kx+b,将点A和点B的坐标代入得:![]() ,解得:k=1,b=﹣1.
,解得:k=1,b=﹣1.
所以直线AB的解析式为y=x﹣1.设点E的坐标为(t,t﹣1),则点F的坐标为(t,![]() ),∴EF=
),∴EF=![]() ﹣(t﹣1)=
﹣(t﹣1)=![]() =
=![]() ,∴当t=﹣
,∴当t=﹣![]() 时,FE取最大值
时,FE取最大值![]() ,此时,点E的坐标为(﹣
,此时,点E的坐标为(﹣![]() ,﹣
,﹣![]() ).
).
(3)存在点P,能使△PEF是以EF为直角边的直角三角形.理由:如图所示:过点F作直线a⊥EF,交抛物线与点P,过点E作直线b⊥EF,交抛物线P′、P″.

由(2)可知点E的坐标为(t,t﹣1),则点F的坐标为(t,![]() ),t=﹣
),t=﹣![]() ,∴点E(﹣
,∴点E(﹣![]() ,﹣
,﹣![]() )、F(﹣
)、F(﹣![]() ,
,![]() ).
).
①当![]() =
=![]() 时,解得:x=﹣
时,解得:x=﹣![]() 或x=﹣
或x=﹣![]() (舍去),∴点P的坐标为(﹣
(舍去),∴点P的坐标为(﹣![]() ,
,![]() ).
).
②当![]() =﹣
=﹣![]() 时,解得:x=﹣1+
时,解得:x=﹣1+![]() 或x=﹣1﹣
或x=﹣1﹣![]() ,∴点P′(﹣1﹣
,∴点P′(﹣1﹣![]() ,﹣
,﹣![]() ),P″(﹣1+
),P″(﹣1+![]() ,﹣
,﹣![]() ).
).
综上所述,点P的坐标为(﹣![]() ,
,![]() )或(﹣1﹣
)或(﹣1﹣![]() ,﹣
,﹣![]() )或(﹣1+
)或(﹣1+![]() ,﹣
,﹣![]() ).
).


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
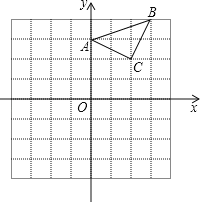
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形ABCD的顶点在格点上,点E是边DC与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)如图1,过点A画线段AF,使AF∥DC,且AF=DC.
(2)如图1,在边AB上画一点G,使∠AGD=∠BGC.
(3)如图2,过点E画线段EM,使EM∥AB,且EM=AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=10,OA与⊙O相交于点P,AB与⊙O切于点B,BP的延长线交直线l于点C.
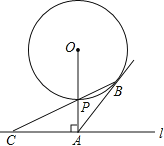
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=4![]() ,求⊙O的半径和线段PB的长.
,求⊙O的半径和线段PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC各顶点坐标分别为A(4,4),B(﹣2,2),C(3,0),

①画出它的以原点O为对称中心的△A'B'C';
②在y轴上有一点P,使BP+C'P最小,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于 x 的一元二次方程 x![]() 2k 1 x k
2k 1 x k![]() k 1 0 有实数根.
k 1 0 有实数根.
(1)求k 的取值范围;
(2)若此方程的两实数根![]() ,
,![]() 满足
满足![]()
![]() 11 ,求k 的值.
11 ,求k 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的调控下,某市的商品房成交均价由今年5月份的每平方米10000元下降到7月份的每平方米8100元.
(1)求6、7两月平均每月降价的百分率;
(2)如果房价继续回落,按此降价的百分率,请你预测到9月份该市的商品房成交均价是否会跌破每平方米6500元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形 ABC 的周长为 10cm,底边 BC 长为 y(cm),腰 AB 长为 x(cm).
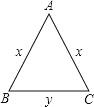
(1)求 y 与 x 之间的函数关系式;
(2)求 x 的取值范围;
(3)腰长 AB=3 时,底边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com