
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,D在AC上,E在BA的延长线上,BD=CE,BD的延长线交CE于点F。求证:BF⊥CE。
科目:初中数学 来源: 题型:
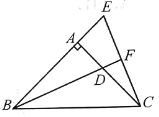
【题目】问题背景:
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠D=90°.E、F分别是BC、CD上的点,且∠EAF=60°.为了探究图中线段BE,EF,FD之间的数量关系,小红的想法是:在EB的延长线上取一点G,使得BG=DF,连接AG,证明△ABG≌△ADF;再证明△AGE≌△AFE,从而得到结论,她的结论是_____________.
探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西40°的A处,舰艇乙在指挥中心南偏东80°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以50海里/小时的速度,同时舰艇乙沿北偏东50°的方向以70海里/小时的速度各自前进2小时后,在指挥中心观测到甲、乙两舰艇分别到达E,F处,两舰艇与指挥中心之间的夹角为70°,则此时两舰艇之间的距离为______海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的.若如果规定向东为正,则行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
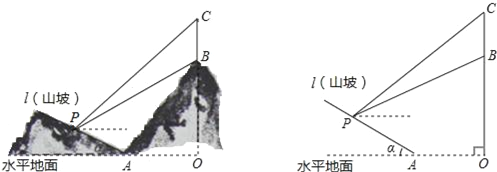
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
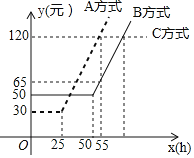
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有射线AP和点B,C,请用尺规按下列要求作图:
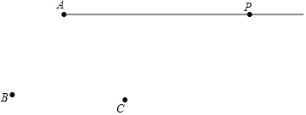
(1)连接AB,并在射线AP上截取AD=AB;
(2)连接BC、BD,并延长BC到E,使BE=BD.
(3)在(2)的基础上,取BE中点F,若BD=6,BC=4,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年9月1日,长春首届航空开放日在长春大房身机场正式举行,空军八一飞行表演队的新换装歼-10飞机,进行了精彩的特技飞行表演,其中一架飞机起飞0.5千米后的高度变化如下表:
高度变化 | 上升4.2 | 下降3.5 | 上升1.4 | 下降1.2 |
记作 | +4.2 | -3.5 | +1.4 | -1.2 |
(1)此时这架飞机飞离地面的高度是多少千米?
(2)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.6干米,下降2.8千米,再上升1.5千米,最后下降0.9千米.若飞机平均上升1干米需消耗6升燃油,平均下降1千米需消耗4升燃油,那么这架飞机在这4个特技表演过程中,一共消耗了多少升燃油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是线段AB的中点,Q为线段PB上一点,分别以AQ、AP、PQ、QB为一边作正方形,其面积对应地记作SACDQ,SAEFP,SPGHQ,SQIJB,设AP=m,QB=n,
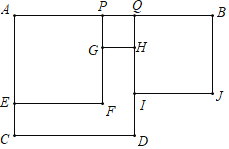
(1)用含有m,n的代数式表示正方形ACDQ的面积SACDQ.
(2)SACDQ+SQIJB与SAEFP+SPGHQ具有怎样的数量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com