练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．计算：$\sqrt{32}$÷$\sqrt{2}$-（π-1）0+|-3|+（$\frac{1}{2}$）-1．

    分析 直接利用利用绝对值以及负指数幂的性质和零指数幂的性质以及二次根式的性质分别化简各数进而得出答案．

    解答 解：$\sqrt{32}$÷$\sqrt{2}$-（π-1）0+|-3|+（$\frac{1}{2}$）-1
    =4$\sqrt{2}$÷$\sqrt{2}$-1+3+2
    =4-1+3+2
    =8．

    点评 此题主要考查了实数运算，正确化简各数是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．如图，平面直角坐标系xOy中，一次函数y=-x+b（b为常数，b＞0）的图象与x轴、y轴分别相交于点A、B，半径为1的⊙O与x轴正半轴相交于点C，与y轴正半轴相交于点D．
    （1）如图1，点E是⊙O上的动点（与点C、D不重合），则∠DEC=45°或135°°．
    （2）当b=$\sqrt{2}$时，直线AB与⊙O相切；当b满足b＞$\sqrt{2}$时，直线AB与⊙O相离；
    （3）如图2，点E是⊙O上的动点，过点E作⊙O的切线交直线AB于点P，连接PO，当b=4时，求PE长的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，在平面直角坐标系中，A（10，0），以OA为直径在第一象限内作半圆，B为半圆上一点，连接AB并延长至C，使BC=AB，过C作CD⊥x轴于点D，交线段OB于点E．已知CD=8，抛物线经过O，E，A三点．
    （1）求直线OB的函数表达式；
    （2）求抛物线的函数表达式；
    （3）若P为抛物线上位于第一象限内的一个动点，以P，O，A，E为顶点的四边形面积记作S，则S取何值时，相应的点P有且只有3个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．对于两个已知图形G1，G2，在G1上任取一点P，在G2上任取一点Q，当线段PQ的长度最小时，我们称这个最小长度为G1，G2的“密距”，用字母d表示；当线段PQ的长度最大时，我们称这个最大的长度为图形G1，G2的“疏距”，用字母f表示．例如，当M（1，2），N（2，2）时，点O与线段MN的“密距”为$\sqrt{5}$，点O与线段MN的“疏距”为2$\sqrt{2}$．
    （1）已知，在平面直角坐标系xOy中，A（-2，0），B（0，4），C（2，0），D（0，1），
    ①点O与线段AB的“密距”为$\frac{4\sqrt{5}}{5}$，“疏距”为4；
    ②线段AB与△COD的“密距”为$\frac{3\sqrt{5}}{5}$，“疏距”为2$\sqrt{5}$；
    （2）直线y=2x+b与x轴，y轴分别交于点E，F，以C（0，-1）为圆心，1为半径作圆，当⊙C与线段EF的“密距”0＜d＜1时，求⊙C与线段EF的“疏距”f的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．某景区的三个景点A，B，C在同一线路上，甲、乙两名游客从景点A出发，甲步行到景点C，乙乘景区观光车先到景点B，在B处停留一段时间后，再步行到景点C．甲、乙两人离开景点A后的路程S（米）关于时间t（分钟）的函数图象如图所示．
    根据以上信息回答下列问题：
    （1）乙出发后多长时间与甲相遇？
    （2）若当甲到达景点C时，乙与景点C的路程为360米，则乙从景点B步行到景点C的速度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．若（a-3）2+|b-6|=0，则以a、b为边长的等腰三角形的周长为（　　）
    A．12B．15C．12或15D．18

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．如图为某物体简化的主视图和俯视图，猜想该物体可能是（　　）
    A．光盘B．双层蛋糕C．游泳圈D．铅笔

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，某校在开展积极培育和践行社会主义核心价值观的活动中，小光同学将自己需要加强的“文明”、“友善”、“法治”、“诚信”的价值取向文字分别贴在4张质地、大小完全一样的硬纸板上，制成卡片，随时提醒自己要做个遵纪守法的好学生．小光同学还把卡片编成一道数学题考同桌小亮：将这4张卡片洗匀后背面朝上放在桌子上，从中随机抽取一张卡片，不放回，再随机抽取另一张卡片，让小亮同学用列表法或画树状图法，求出两次抽到卡片上的文字含有“文明”、“诚信”价值取向的概率（卡片名称可用字母表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

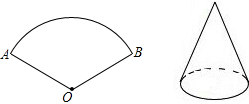    1．如图，将面积为108πcm2，半径为18cm的扇形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（粘连部分忽略不计）则圆锥形纸帽的高是12$\sqrt{2}$cm．

    查看答案和解析>>

    同步练习册答案