
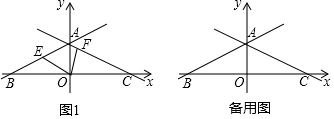
分析 (1)利用直角三角形30度角性质,求出点B坐标,利用待定系数法即可解决问题.
(2)取AC中点G,连接GO,CO,根据△GOE≌△COF,可得GE=CF,即可解题;
(3)结论:BE-CF=$\sqrt{3}$OB=$\frac{\sqrt{3}}{2}$BC.过点O作OM⊥AB于 M,ON⊥AC于N,首先证明△OME≌△ONF,推出EM=FN,Rt△OMB≌Rt△ONC,推出BM=CN,可得BE-CF=BM+EM-(FN-CN)=2BM,因为BC=2OB,BM=$\frac{\sqrt{3}}{2}$OB,由此即可解决问题.
解答 解:(1)∵A(0,2),
∴OA=2,
∵∠ABO=30°,
∴AB=2OA=4,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=2$\sqrt{3}$,
∴B(-2$\sqrt{3}$,0),
设直线AB的解析式为y=kx+b,把A、B两点坐标代入得$\left\{\begin{array}{l}{b=2}\\{-2\sqrt{3}k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=2}\end{array}\right.$,
∴直线AC的解析式为y=$\frac{\sqrt{3}}{3}$x+2,
∵∴直线AC的解析式为y=-$\frac{\sqrt{3}}{3}$x+2.
(2)取AB中点G,连接GO,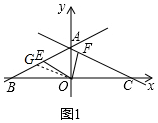
∵AC=AB,O为BC中点,∴AO⊥BC,∠CAO=60°,
∵G为AB中点,
∴OG=$\frac{1}{2}$AB=GA,
∵∠BAC=120°,
∴∠ACB=∠ABC=30°,
∴OA=$\frac{1}{2}$AB,
∴AO=GO,
∴△OGA为等边三角形,
∴∠GOA=60°,
∵∠EOF=60°
∴∠GOE=∠AOF,
在△GOE和△AOF中,
$\left\{\begin{array}{l}{∠EGO=∠FAO}\\{∠EOG=∠AOF}\\{OG=OA}\end{array}\right.$,
∴△GOE≌△AOF(AAS),
∴GE=AF,
∴AF+AE=AE+GE=AG=$\frac{1}{2}$AB,
∴BE+CF=AB+AC-(AE+AF)=2AB-$\frac{1}{2}$AB=$\frac{3}{2}$AB=6.
(3)结论:BE-CF=$\sqrt{3}$OB=$\frac{\sqrt{3}}{2}$BC.
理由:过点O作OM⊥AB于 M,ON⊥AC于N,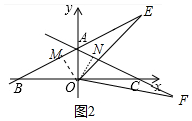
∵∠EAF=∠EOF=60°,
∴∠E=∠F,
∵OA平分∠BAC,OM⊥AB,ON⊥AC,
∴OM=ON,
在△OME和△ONF中,
$\left\{\begin{array}{l}{∠E=∠F}\\{∠OME=∠ONF}\\{OM=ON}\end{array}\right.$,
∴△OME≌△ONF,
∴EM=FN,
∵OB=OC,OM=ON,
∴Rt△OMB≌Rt△ONC,
∴BM=CN,
∴BE-CF=BM+EM-(FN-CN)=2BM,
∵BC=2OB,BM=$\frac{\sqrt{3}}{2}$OB,
∴BE-CF=$\sqrt{3}$OB=$\frac{\sqrt{3}}{2}$BC.
点评 此题考查了全等三角形的判定与性质、等腰直角三角形的性质以及含30°角的直角三角形的性质.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
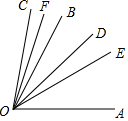 已知∠BOC在∠AOB的外部,OE平分∠AOB,OF平分∠BOC,OD平分∠AOC,∠AOE=30°,∠BOD=20°,试求∠COF的度数,下面是李小雨同学的解题过程:
已知∠BOC在∠AOB的外部,OE平分∠AOB,OF平分∠BOC,OD平分∠AOC,∠AOE=30°,∠BOD=20°,试求∠COF的度数,下面是李小雨同学的解题过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
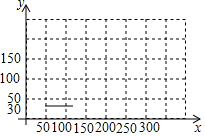 某电信公司提供的移动通讯服务的收费标准有两种方案,如表所示:
某电信公司提供的移动通讯服务的收费标准有两种方案,如表所示:| A方案 | B方案 | |
| 每月基本服务费 | 30元 | 50元 |
| 每月免费通话时间 | 120分 | 200分 |
| 超出后每分钟收费 | 0.4元 | 0.4元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
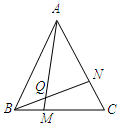 (1)学完全等三角形以后,老师布置了这样一道题:如图,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q.求证:∠BQM=60°.(注意:等边三角形三条边都相等,每个内角都是60°)
(1)学完全等三角形以后,老师布置了这样一道题:如图,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q.求证:∠BQM=60°.(注意:等边三角形三条边都相等,每个内角都是60°)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com