
【题目】为实现区域教育均衡发展,我市计划对某县![]() 、
、![]() 两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所
两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所![]() 类学校和两所
类学校和两所![]() 类学校共需资金230万元;改造两所
类学校共需资金230万元;改造两所![]() 类学校和一所
类学校和一所![]() 类学校共需资金205万元.
类学校共需资金205万元.
(1)改造一所![]() 类学校和一所
类学校和一所![]() 类学校所需的资金分别是多少万元?
类学校所需的资金分别是多少万元?
(2)若该县的![]() 类学校不超过5所,则
类学校不超过5所,则![]() 类学校至少有多少所?
类学校至少有多少所?
(3)我市计划今年对该县![]() 、
、![]() 两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到
两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到![]() 、
、![]() 两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
【答案】(1)![]() (2)若该县的
(2)若该县的![]() 类学校不超过5所,则
类学校不超过5所,则![]() 类学校至少有15所.
类学校至少有15所.
(3)共有4种方案.
【解析】
(1)可根据“改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B类学校共需资金205万元”,列出方程组求出答案;
(2)根据“共需资金1575万元”“A类学校不超过5所”,进行判断即可;
(3)要根据“若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元”来列出不等式组,判断出不同的改造方案;
解:(1)设改造一所A类学校和一所B类学校所需的改造资金分别为a万元和b万元.
依题意得:![]() ,
,
解得:![]() ,
,
答:改造一所A类学校和一所B类学校所需的改造资金分别为60万元和85万元;
(2)设该县有A、B两类学校分别为m所和n所.
则60m+85n=1575,
m=![]() ,
,
∵A类学校不超过5所,
∴![]() ,
,
∴15≤n<18,
∵n为整数,
∴n=15,16,17.
当n=15,m=5符合题意,
即:B类学校至少有15所;
(3)设今年改造A类学校x所,则改造B类学校为(6-x)所,
依题意得:![]() ,
,
解得:1≤x≤4,
∵x取整数
∴x=1,2,3,4
答:共有4种方案.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
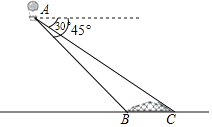
【题目】汉江是长江最长的支流,在历史上占居重要地位,陕西省境内的汉江为汉江上游段.李琳利用热气球探测器测量汉江某段河宽,如图,探测器在A处观测到正前方汉江两岸岸边的B、C两点,并测得B、C两点的俯角分别为45°,30°已知A处离地面的高度为80m,河平面BC与地面在同一水平面上,请你求出汉江该段河宽BC.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为阻断疫情向校园蔓延,确保师生生命安全和身体健康,教育部2020年1月29日下发通知,要求今年春季学期延期开学,“停课不停学”,统筹利用网络电视资源进行教学,某校为了让学生能够达到最佳的学习效果,确定老师们可以选用以下三种直播授课方式:A.智慧云直播,B.钉钉直播,C.腾讯会议直播.
(1)张明老师从三种网络授课方式中随机选取一种,是智慧云直播的概率为 ;
(2)张明和李刚两位老师从中随机各选取一种网络直播方式进行授课,请你用列表法或画树状图法,求出张明和李刚两位老师选取不同的网络直播授课方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,其对称轴是直线
两点,其对称轴是直线![]() ,抛物线与
,抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() ,线段
,线段![]() 与
与![]() 轴交于点
轴交于点![]() .
.
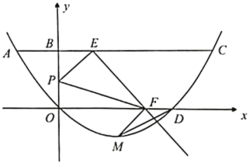
(1)求抛物线的解析式,并写出点![]() 的坐标;
的坐标;
(2)若点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,点
,点![]() 为线段
为线段![]() 上不与端点重合的动点,连接
上不与端点重合的动点,连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,探究在
,探究在![]() 点运动过程中,线段
点运动过程中,线段![]() ,
,![]() 有何数量关系?并证明所探究的结论;
有何数量关系?并证明所探究的结论;
(3)设抛物线顶点为![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在研究抛物线![]() (
(![]() 为常数)时,得到如下结论,其中正确的是( )
为常数)时,得到如下结论,其中正确的是( )
A.无论![]() 取何实数,
取何实数,![]() 的值都小于0
的值都小于0
B.该抛物线的顶点始终在直线![]() 上
上
C.当![]() 时,
时,![]() 随
随![]() 的增大而增大,则
的增大而增大,则![]()
D.该抛物线上有两点![]() ,
,![]() ,若
,若![]() ,
,![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”;
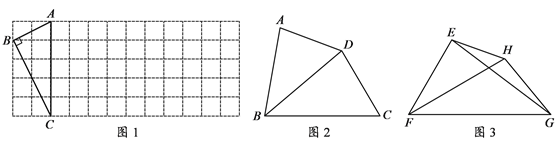
理解:
⑴ 如图1,△ABC的三个顶点均在正方形网格中的格点上,若四边形ABCD是以AC为“相似对角线”的四边形,请用无刻度的直尺在网格中画出点D(保留画图痕迹,找出3个即可);
⑵ 如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC. 请问BD是四边形ABCD的“相似对角线”吗?请说明理由;
运用:
⑶ 如图3,已知FH是四边形EFGH的“相似对角线”, ∠EFH=∠HFG=30°.连接EG,若△EFG的面积为![]() ,求FH 的长.
,求FH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点P是直线BC上方抛物线上的一动点,PE∥y轴,交直线BC于点E连接AP,交直线BC于点 D.
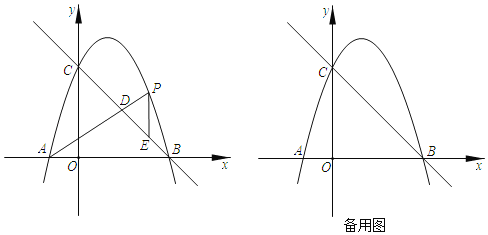
(1)求抛物线的函数表达式;
(2)当AD=2PD时,求点P的坐标;
(3)求线段![]() 的最大值;
的最大值;
(4)当线段![]() 最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.
最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com