
【题目】阅读理解填空,并在括号内填注理由.
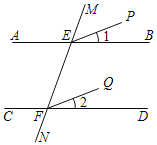
如图,已知AB∥CD,M,N分别交AB,CD于点E,F,∠1=∠2,求证:EP∥FQ.
证明:∵AB∥CD( )
∴∠MEB=∠MFD( ).
又∵∠1=∠2( )
∠MEB﹣∠1=∠MFD﹣∠2( )
即:∠MEP=∠
EP∥ .( )
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某汽车行驶时油箱中余油量Q(升)与行驶时间t(小时)的关系如下表:
行驶时间t | 1 | 2 | 3 | 4 | … |
余油量Q | 40﹣6 | 40﹣12 | 40﹣18 | 40﹣24 | … |
(1)写出用行驶时间t表示余油量Q的代数式 ;
(2)当t=![]() 时,余油量Q的值为 升;
时,余油量Q的值为 升;
(3)汽车每小时行驶60公里,问油箱中原有汽油可供汽车行驶多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段MN=8,C是线段MN上一动点,在MN的同侧分别作等边△CMD和等边△CNE.
(1)如图①,连接DN与EM,两条线段相交于点H,求证ME=DN,并求∠DHM的度数;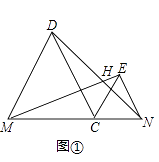
(2)如图②,过点D、E分别作线段MN的垂线,垂足分别为F、G,问:在点C运动过程中,DF+EG的长度是否为定值,如果是,请求出这个定值,如果不是请说明理由;
(3)当点C由点M移到点N时,点H移到的路径长度为(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( ) 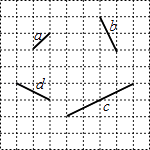
A.3种
B.6种
C.8种
D.12种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点M、N同时从原点出发沿数轴做匀速运动,己知动点M、N的运动速度比是1:2(速度单位:1个单位长度/秒),设运动时间为t秒.
![]()
(1)若动点M向数轴负方向运动,动点N向数轴正方向运动,当t=2秒时,动点M运动到A点,动点N运动到B点,且AB=12(单位长度).
①在直线l上画出A、B两点的位置,并回答:点A运动的速度是 (单位长度/秒);点B运动的速度是 (单位长度/秒).
②若点P为数轴上一点,且PA﹣PB=OP,求![]() 的值;
的值;
(2)由(1)中A、B两点的位置开始,若M、N同时再次开始按原速运动,且在数轴上的运动方向不限,再经过几秒,MN=4(单位长度)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9
(1)求证:△COD∽△CBE;
(2)求半圆O的半径 ![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com