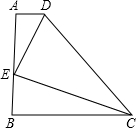
直角梯形ABCD中,AD∥BC,AB=AD=3,边BC,AB分别在x轴和y轴上,已知点C的坐标分别为(4,0).动点P从B点出发,以每秒1个单位的速度沿BC方向作匀速直线运动,同时点Q从D点出发,以与P点相同的速度沿DA方向运动,当Q点运动到A点时,P,Q两点同时停止运动.设点P运动时间为t,
(1)求线段CD的长.
(2)连接PQ交直线AC于点E,当AE:EC=1:2时,求t的值,并求出此时△PEC的面积.
(3)过Q点作垂直于AD的射线交AC于点M,交BC于点N,连接PM,
①是否存在某一时刻,使以M、P、C三点为顶点的三角形是等腰三角形?若存在,求出此时t的值;若不存在,请说明理由;
②当t=______时,点P、M、D在同一直线上.(直接写出)
【答案】
分析:(1)过点D作DF⊥BC与F,可得四边形ABFD是正方形,然后求出DF=AB,BF=AD,再求出FC,再根据勾股定理列式进行计算即可求出CD;
(2)用t表示出AQ、CP,再根据AD∥BC求出△AQE和△CPE相似,根据相似三角形对应边成比例列出比例式进行计算求出t的值,再求出PC的长以及点E到PC的距离,然后利用三角形的面积公式列式进行计算即可得解;
(3)①先用t表示出MC、PC,然后分PC=MC,MP=MC,MP=PC三种情况,分别根据等腰三角形三线合一的性质列出方程求解即可得到相应的t值;
②用t表示出QD、PN,再根据相似三角形对应边成比例列出比例式求解即可得到t的值.
解答:解:(1)

如图,过点D作DF⊥BC与F,
∵四边形ABCD是直角梯形,AB=AD=3,
∴四边形ABFD是正方形,
∴DF=AB=3,BF=AD=3,
∵点C的坐标分别为(4,0),
∴OC=4,
∴FC=BC-BF=4-3=1,
∴CD=

=
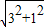
=
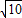
;
(2)∵P、Q的速度都是每秒1个单位,
∴AQ=3-t,CP=4-t,
∵AD∥BC,
∴△AQE∽△CPE,
∴
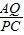
=
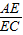
=

,
即
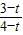
=

,
解得t=2,
∴PC=BC-BP=4-2=2,
∵AE:EC=1:2,
∴点E到BC的距离为
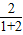
AB=

×3=2,
∴S
△PEC=

×2×2=2;
(3)①存在.
根据勾股定理,AC=

=
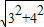
=5,
CN=BC-BN=4-(3-t)=1+t,
cos∠ACB=

=
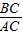
,
即
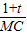
=

,
解得MC=

(1+t),
PC=BC-BP=4-t,
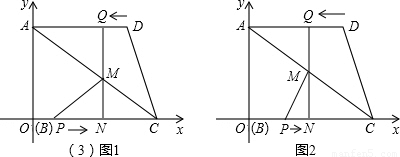
如图1,若MP=MC,则PN=CN,
∴(3-t)-t=1+t,
解得t=

;
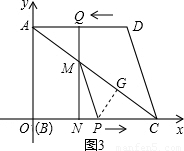
如图2,若PC=MC,则4-t=

(1+t),
解得t=
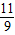
;
如图3,若MP=MC,过点P作PG⊥AC于G,
则cos∠ACB=

=
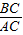
,
即
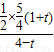
=

,
解得t=
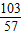
;
综上所述,t为

秒或
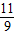
秒或
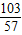
时,以M、P、C三点为顶点的三角形是等腰三角形;
②如图4,当点P、M、D在同一直线上时,
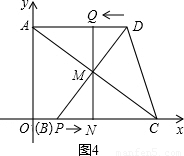
∵AD∥BC,
∴△DQM∽PNM,△ADM∽△CPM,
∴
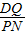
=

,

=
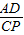
,
∴
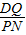
=
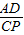
,
∵PN=BN-BP=AQ-BP=3-t-t=3-2t,
∴
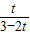
=

,
整理得,t
2-10t+9=0,
解得t
1=1,t
2=9(舍去),
所以,t=1时,点P、M、D在同一直线上.
点评:本题是相似形综合题,主要考查了直角梯形的性质,勾股定理,相似三角形的判定与性质,等腰三角形的性质,(3)①要根据等腰三角形的腰长分情况讨论,②根据两对相似三角形的过渡量
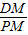
得到比例式是解题的关键.

 如图,过点D作DF⊥BC与F,
如图,过点D作DF⊥BC与F, =
=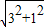 =
=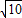 ;
;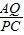 =
=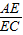 =
= ,
,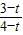 =
= ,
,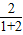 AB=
AB= ×3=2,
×3=2, ×2×2=2;
×2×2=2; =
=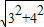 =5,
=5, =
=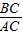 ,
,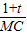 =
= ,
, (1+t),
(1+t),

 ;
; (1+t),
(1+t),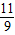 ;
; =
=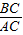 ,
,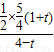 =
= ,
,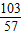 ;
; 秒或
秒或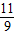 秒或
秒或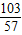 时,以M、P、C三点为顶点的三角形是等腰三角形;
时,以M、P、C三点为顶点的三角形是等腰三角形; ∵AD∥BC,
∵AD∥BC,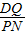 =
= ,
, =
=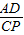 ,
,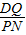 =
=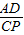 ,
,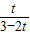 =
= ,
, 得到比例式是解题的关键.
得到比例式是解题的关键. 

 下结论:
下结论: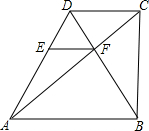 EF∥AB,交AD于点E,CF=4cm.
EF∥AB,交AD于点E,CF=4cm.