
°æƒø°ø—ß–£ ˝—ß…ÁÕ≈µƒÕ¨—ß√«‘⁄—ß…˙÷–ø™’π°∞¡ÀΩ‚–£—µ“‚“°±µƒµ˜≤ȪÓ∂Ø£Æ≤…»°Àʪ˙≥È—˘µƒ∑Ω ΩΩ¯––Œ æ̵˜≤ȣƌ æ̵˜≤ȵƒΩ·π˚∑÷Œ™![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Àƒ¿ý£Æ
Àƒ¿ý£Æ![]() ¿ý±Ì æ∑«≥£¡ÀΩ‚£ª
¿ý±Ì æ∑«≥£¡ÀΩ‚£ª![]() ¿ý±Ì æ±»Ωœ¡ÀΩ‚£ª
¿ý±Ì æ±»Ωœ¡ÀΩ‚£ª![]() ¿ý±Ì æª˘±æ¡ÀΩ‚£ª
¿ý±Ì æª˘±æ¡ÀΩ‚£ª![]() ¿ý±Ì æ≤ªÃ´¡ÀΩ‚£Æ£®“™«Û√øŒªÕ¨—ß±ÿ–Η°≤¢«“÷ªƒÐ—°‘Ò“ªœÓ£©Õ≥º∆ ˝æð’˚¿Ì»Á±Ì£∫
¿ý±Ì æ≤ªÃ´¡ÀΩ‚£Æ£®“™«Û√øŒªÕ¨—ß±ÿ–Η°≤¢«“÷ªƒÐ—°‘Ò“ªœÓ£©Õ≥º∆ ˝æð’˚¿Ì»Á±Ì£∫
¿ý± | ∆µ ˝ | ∆µ¬ |
| 20 |
|
|
| 0.3 |
| 11 | 0.22 |
| 4 | 0.08 |
£®1£©±Ì÷–![]() __________£ª
__________£ª![]()
£®2£©∏˘æð±Ì÷– ˝æ𣨫Û≥ˆ![]() ¿ýÕ¨—ß ˝À˘∂‘”¶µƒ…»–Œ‘≤–ƒΩ«Œ™_________∂»£Æ
¿ýÕ¨—ß ˝À˘∂‘”¶µƒ…»–Œ‘≤–ƒΩ«Œ™_________∂»£Æ
£®3£©∏˘æðµ˜≤ÈΩ·π˚£¨«Îƒ„π¿º∆∏√–£1500√˚—ß…˙÷–∂‘–£—µ°∞∑«≥£¡ÀΩ‚°±µƒ»À ˝£ª
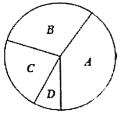
£®4£©—ß–£‘⁄ø™’π¡ÀΩ‚–£—µ“‚“ªÓ∂Ø÷–£¨–Ë“™¥”![]() ¿ýµƒº◊°¢““°¢±˚°¢∂°Àƒ√˚Õ¨—ß÷–Àʪ˙—°»°2»À≤Œº”’π æªÓ∂Ø£¨«Û«°∫√—°÷–º◊““¡Ω»Àµƒ∏≈¬ £ø£®«Î”√¡–±Ì∑®ªÚ « ˜◊¥Õº±Ì 棩
¿ýµƒº◊°¢““°¢±˚°¢∂°Àƒ√˚Õ¨—ß÷–Àʪ˙—°»°2»À≤Œº”’π æªÓ∂Ø£¨«Û«°∫√—°÷–º◊““¡Ω»Àµƒ∏≈¬ £ø£®«Î”√¡–±Ì∑®ªÚ « ˜◊¥Õº±Ì 棩
°æ¥∞∏°ø£®1£©15£¨0.4£ª£®2£©108£ª£®3£©600»À£ª£®4£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©œ»∏˘æðD¿ýµƒ∆µ ˝”Î∆µ¬ «Û≥ˆ◊Ð∆µ ˝£¨‘Ÿ∏˘æð°∞∆µ¬ ![]() ∆µ ˝
∆µ ˝![]() ◊Ð∆µ ˝°±ø…µ√A¿ýµƒ∆µ¬ £¨”√◊Ð∆µ ˝ºı»•A°¢C°¢D»˝¿ýµƒ∆µ ˝º¥ø…µ√B¿ýµƒ∆µ ˝£ª
◊Ð∆µ ˝°±ø…µ√A¿ýµƒ∆µ¬ £¨”√◊Ð∆µ ˝ºı»•A°¢C°¢D»˝¿ýµƒ∆µ ˝º¥ø…µ√B¿ýµƒ∆µ ˝£ª
£®2£©¿˚”√B¿ýÕ¨—ßµƒ∆µ¬ ≥À“‘![]() º¥ø…µ√£ª
º¥ø…µ√£ª
£®3£©°∞∑«≥£¡ÀΩ‚°±∂‘”¶µƒ «A¿ý£¨¿˚”√A¿ýµƒ∆µ¬ ≥À“‘1500º¥ø…µ√£ª
£®4£©œ»ª≠≥ˆ ˜◊¥Õº£¨‘Ÿµ√≥ˆ°∞¥”![]() ¿ýµƒº◊°¢““°¢±˚°¢∂°Àƒ√˚Õ¨—ß÷–Àʪ˙—°»°2»À≤Œº”’π æªÓ∂Ø°±µƒÀ˘”–ø…ƒÐµƒΩ·π˚£¨“‘º∞°∞«°∫√—°÷–º◊““¡Ω»À°±µƒΩ·π˚£¨»ª∫Û¿˚”√∏≈¬ π´ Ωº∆À„º¥ø…£Æ
¿ýµƒº◊°¢““°¢±˚°¢∂°Àƒ√˚Õ¨—ß÷–Àʪ˙—°»°2»À≤Œº”’π æªÓ∂Ø°±µƒÀ˘”–ø…ƒÐµƒΩ·π˚£¨“‘º∞°∞«°∫√—°÷–º◊““¡Ω»À°±µƒΩ·π˚£¨»ª∫Û¿˚”√∏≈¬ π´ Ωº∆À„º¥ø…£Æ
£®1£©◊Ð∆µ ˝Œ™![]()
‘Ú![]()
![]()
π ¥∞∏Œ™£∫15£¨![]() £ª
£ª
£®2£©![]() ¿ýÕ¨—ß ˝À˘∂‘”¶µƒ…»–Œ‘≤–ƒΩ«Œ™
¿ýÕ¨—ß ˝À˘∂‘”¶µƒ…»–Œ‘≤–ƒΩ«Œ™![]()
π ¥∞∏Œ™£∫108£ª
£®3£©°∞∑«≥£¡ÀΩ‚°±∂‘”¶µƒ «A¿ý£¨![]()
‘Ú![]() £®»À£©
£®»À£©
¥£∫∏√–£1500√˚—ß…˙÷–∂‘–£—µ°∞∑«≥£¡ÀΩ‚°±µƒ»À ˝Œ™600»À£ª
£®4£©”…“‚£¨ª≠≥ˆ ˜◊¥Õº»Áœ¬À˘ æ£∫

“Ú¥À£¨¥”![]() ¿ýµƒº◊°¢““°¢±˚°¢∂°Àƒ√˚Õ¨—ß÷–Àʪ˙—°»°2»À≤Œº”’π æªÓ∂صƒÀ˘”–ø…ƒÐµƒΩ·π˚π≤12÷÷Ω·π˚£¨À¸√«√ø“ª÷÷Ω·π˚≥ˆœ÷µƒø…ƒÐ–‘∂ºœýµ»£¨∆‰÷–£¨«°∫√—°÷–º◊““¡Ω»ÀµƒΩ·π˚π≤2÷÷
¿ýµƒº◊°¢““°¢±˚°¢∂°Àƒ√˚Õ¨—ß÷–Àʪ˙—°»°2»À≤Œº”’π æªÓ∂صƒÀ˘”–ø…ƒÐµƒΩ·π˚π≤12÷÷Ω·π˚£¨À¸√«√ø“ª÷÷Ω·π˚≥ˆœ÷µƒø…ƒÐ–‘∂ºœýµ»£¨∆‰÷–£¨«°∫√—°÷–º◊““¡Ω»ÀµƒΩ·π˚π≤2÷÷
‘ÚÀ˘«Ûµƒ∏≈¬ Œ™![]() £Æ
£Æ


 »´ƒÐ¡∑øºæÌœµ¡–¥∞∏
»´ƒÐ¡∑øºæÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþy£Ω![]() x2+
x2+![]() x©Å4”Îx÷·Ωª”⁄A°¢B¡Ωµ„£®µ„A‘⁄µ„Bµƒ◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„C£Æ
x©Å4”Îx÷·Ωª”⁄A°¢B¡Ωµ„£®µ„A‘⁄µ„Bµƒ◊Û≤ý£©£¨”Îy÷·Ωª”⁄µ„C£Æ
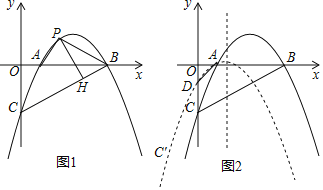
£®1£©¡¨Ω”BC£¨P «œþ∂ŒBC…œ∑Ω≈◊ŒÔœþ…œµƒ“ª∂ص„£¨π˝µ„P◊˜PH°ÕBC”⁄µ„H£¨µ±PH≥§∂»◊Ó¥Û ±£¨‘⁄°˜APBƒ⁄≤ø”–“ªµ„M£¨¡¨Ω”AM°¢BM°¢PM£¨«ÛAM+![]() BM+PMµƒ◊Ó–°÷µ£Æ
BM+PMµƒ◊Ó–°÷µ£Æ
£®2£©»Ùµ„D «OCµƒ÷–µ„£¨Ω´≈◊ŒÔœþy£Ω![]() x2+
x2+![]() x©Å4—ÿ…‰œþAD∑ΩœÚ∆Ω“∆
x©Å4—ÿ…‰œþAD∑ΩœÚ∆Ω“∆![]() ∏ˆµ•Œªµ√µΩ–¬≈◊ŒÔœþy°‰£¨C°‰ «≈◊ŒÔœþy°‰…œ”ÎC∂‘”¶µƒµ„£¨≈◊ŒÔœþy'µƒ∂‘≥∆÷·…œ”–“ª∂ص„N£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷– «∑ҥʑ⁄“ªµ„S£¨ πµ√C°‰°¢N°¢B°¢SŒ™∂•µ„µƒÀƒ±þ–Œ «æÿ–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Sµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
∏ˆµ•Œªµ√µΩ–¬≈◊ŒÔœþy°‰£¨C°‰ «≈◊ŒÔœþy°‰…œ”ÎC∂‘”¶µƒµ„£¨≈◊ŒÔœþy'µƒ∂‘≥∆÷·…œ”–“ª∂ص„N£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷– «∑ҥʑ⁄“ªµ„S£¨ πµ√C°‰°¢N°¢B°¢SŒ™∂•µ„µƒÀƒ±þ–Œ «æÿ–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Sµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄’˝∑Ω–Œ![]() ÷–£¨
÷–£¨![]() µƒ∂•µ„
µƒ∂•µ„![]() £¨
£¨![]() ∑÷±‘⁄
∑÷±‘⁄![]() £¨
£¨![]() ±þ…œ£¨∏þ
±þ…œ£¨∏þ![]() ”Î’˝∑Ω–Œµƒ±þ≥§œýµ»£¨¡¨Ω”
”Î’˝∑Ω–Œµƒ±þ≥§œýµ»£¨¡¨Ω”![]() ∑÷±Ωª
∑÷±Ωª![]() £¨
£¨![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() £¨œ¬¡–Àµ∑®£∫¢Ÿ
£¨œ¬¡–Àµ∑®£∫¢Ÿ![]() £ª¢⁄¡¨Ω”
£ª¢⁄¡¨Ω”![]() £¨
£¨![]() £¨‘Ú
£¨‘Ú![]() Œ™÷±Ω«»˝Ω«–Œ£ª¢€
Œ™÷±Ω«»˝Ω«–Œ£ª¢€![]() £ª¢Ð»Ù
£ª¢Ð»Ù![]() £¨
£¨![]() £¨‘Ú
£¨‘Ú![]() µƒ≥§Œ™
µƒ≥§Œ™![]() £¨∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝ «£® £©
£¨∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝ «£® £©
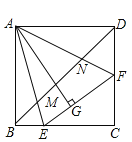
A.4B.3C.2D.1
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº£¨÷±œþ![]() Ωª◊¯±Í÷·”⁄A°¢C¡Ωµ„£¨≈◊ŒÔœþ
Ωª◊¯±Í÷·”⁄A°¢C¡Ωµ„£¨≈◊ŒÔœþ![]() π˝A°¢C¡Ωµ„£Æ
π˝A°¢C¡Ωµ„£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©»Ùµ„PŒ™≈◊ŒÔœþŒª”⁄µ⁄»˝œÛœÞ…œ“ª∂ص„£¨¡¨Ω”PA£¨PC£¨ ‘Œ °˜PAC «∑ҥʑ⁄◊Ó¥Û÷µ£¨»Ù¥Ê‘⁄£¨«Î«Û≥ˆ°˜APC»°◊Ó¥Û÷µ“‘º∞µ„Pµƒ◊¯±Í£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£ª
£®3£©µ„MŒ™≈◊ŒÔœþ…œ“ªµ„£¨µ„NŒ™≈◊ŒÔœþ∂‘≥∆÷·…œ“ªµ„£¨»Ù°˜NMC «“‘°œNMCŒ™÷±Ω«µƒµ»—¸÷±Ω«»˝Ω«–Œ£¨«Î÷±Ω”–¥≥ˆµ„Mµƒ◊¯±Í£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ Â÷≥ˆ£∫
£®1£©»ÁÕº¢Ÿ‘⁄![]() ÷–£¨
÷–£¨![]() «
«![]() ±þ
±þ![]() µƒ∏þ£¨µ„
µƒ∏þ£¨µ„![]() «
«![]() …œ»Œ“‚“ªµ„£¨»Ù
…œ»Œ“‚“ªµ„£¨»Ù![]() ‘Ú
‘Ú![]() µƒ◊Ó–°÷µŒ™_°°°°°°°°£ª
µƒ◊Ó–°÷µŒ™_°°°°°°°°£ª
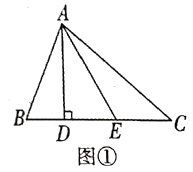
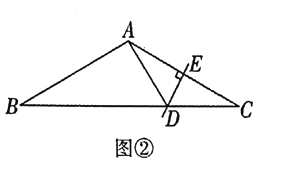
£®2£©»ÁÕº¢⁄£¨‘⁄µ»—¸![]() ÷–£¨
÷–£¨![]() «
«![]() µƒ¥π÷±∆Ω∑÷œþ£¨∑÷±Ωª
µƒ¥π÷±∆Ω∑÷œþ£¨∑÷±Ωª![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ÷Ð≥§£ª
µƒ÷Ð≥§£ª
Œ Ã‚Ω‚æˆ£∫
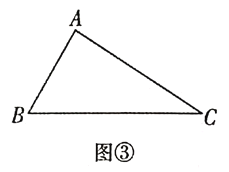
£®3£©»ÁÕº¢€£¨ƒ≥π´‘∞πп̑±ƒ‚‘⁄‘∞ƒ⁄πʪƓª∏ˆ![]() «¯”Ú÷÷÷≤ª®ªÐ£¨«“Œ™∑Ω±„”ŒøÕ”Œ¿¿£¨”˚‘⁄∏˜∂•µ„÷ƺ‰πʪƵ¿¬∑
«¯”Ú÷÷÷≤ª®ªÐ£¨«“Œ™∑Ω±„”ŒøÕ”Œ¿¿£¨”˚‘⁄∏˜∂•µ„÷ƺ‰πʪƵ¿¬∑![]() ∫Õ
∫Õ![]() £¨¬˙◊„
£¨¬˙◊„![]() µ„
µ„![]() µΩ
µΩ![]() µƒæý¿ÎŒ™
µƒæý¿ÎŒ™![]() .Œ™¡ÀΩ⁄‘º≥…±æ£¨“™ πµ√
.Œ™¡ÀΩ⁄‘º≥…±æ£¨“™ πµ√![]() ÷Æ∫Õ◊Ó∂㨠‘«Û
÷Æ∫Õ◊Ó∂㨠‘«Û![]() µƒ◊Ó–°÷µ(¬∑øÌ∫ˆ¬‘≤ªº∆)£Æ
µƒ◊Ó–°÷µ(¬∑øÌ∫ˆ¬‘≤ªº∆)£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ„![]() ‘⁄“ªÃı÷±œþ…œ£¨
‘⁄“ªÃı÷±œþ…œ£¨![]() ,
,![]() °Œ
°Œ![]() £¨
£¨![]() £Æ
£Æ
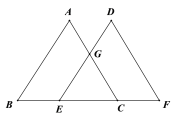
£®1£©«Û÷§£∫![]()
£®2£©»Ù![]() °„£¨«Û
°„£¨«Û![]() µƒ¥Û–°£Æ
µƒ¥Û–°£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
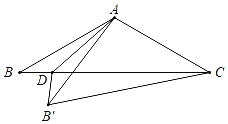
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨AB£ΩAC£Ω![]() £¨°œB£Ω30°„£¨D «BC…œ“ªµ„£¨¡¨Ω”AD£¨∞—°˜ABD—ÿ÷±œþAD’€µ˛£¨µ„B¬‰‘⁄B°‰¥¶£¨¡¨Ω”B'C£¨»Ù°˜AB'C «÷±Ω«»˝Ω«–Œ£¨‘ÚBDµƒ≥§Œ™_____£Æ
£¨°œB£Ω30°„£¨D «BC…œ“ªµ„£¨¡¨Ω”AD£¨∞—°˜ABD—ÿ÷±œþAD’€µ˛£¨µ„B¬‰‘⁄B°‰¥¶£¨¡¨Ω”B'C£¨»Ù°˜AB'C «÷±Ω«»˝Ω«–Œ£¨‘ÚBDµƒ≥§Œ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº“◊°÷ÿ«Ï¡Ωœý¡⁄–°«¯µƒ–°√˜∫Õ–°ª™‘⁄“ª¥Œ ˝—ßøŒ∫Û£¨Ω¯––¡À“ª¥Œ ˝—ß µº˘ªÓ∂أƻÁÕº£¨‘⁄Õ¨“ªÀÆ∆Ω√Ê¥”◊ÛÕ˘”““¿¥Œ «–°√˜º“À˘‘⁄µƒæ”√Ò¬•°¢–°ª™º“À˘‘⁄µƒ–°—Û∑ø°¢±≥øø–°ª™º“µƒ“ª◊˘–°…Ω£¨ µº˘ƒ⁄»ðŒ™≤‚¡ø–°…Ωµƒ∏þ∂»£¨º“◊°∂•¬•µƒ–°√˜‘⁄¥∞ªßA¥¶≤‚µ√–°…Ω…Ω∂•µƒ“ªø√¥Û ˜∂•∂ÀEµƒ∏©Ω«Œ™10°„£¨–°ª™‘⁄◊‘º“¬•œ¬C¥¶≤‚µ√–°√˜º“¥∞ªßA¥¶µƒ—ˆΩ«Œ™37°„£¨«“≤‚µ√∆¬√ÊCDµƒ∆¬∂»i£Ω1£∫2£¨“—÷™¡Ωº“ÀÆ∆Ωæý¿ÎBC£Ω120√◊£¨¥Û ˜∏þ∂»DE£Ω3√◊£¨‘Ú–°…Ω…Ω∂•DµΩÀÆ∆Ω√ÊBFµƒ¥π÷±∏þ∂»‘ºŒ™£® £©£®æ´»∑µΩ0.1√◊£¨≤Œøº ˝æðsin37°„°÷![]() £¨tan37°„°÷
£¨tan37°„°÷![]() £¨sin10°„°÷
£¨sin10°„°÷![]() £¨tan10°„°÷
£¨tan10°„°÷![]() £©
£©

A.55.0√◊B.50.3√◊C.48.1 √◊D.57.3√◊
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
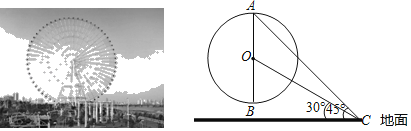
°æƒø°ø°∞ÃÏø’÷Æ≥«°±ƒ¶ÃϬ÷£¨Œª”⁄ƒ˛≤® –∫º÷ðÕ–¬«¯ª∂¿÷ ¿ΩÁ£Æƒ¶ÃϬ÷∏þ‘º126√◊£®◊Ó∏þµ„µΩµÿ√ʵƒæý¿Î£©£Æ»ÁÕº£¨µ„O «ƒ¶ÃϬ÷µƒ‘≤–ƒ£¨AB «∆‰¥π÷±”⁄µÿ√ʵƒ÷±æ∂£¨–°√˜‘⁄µÿ√ÊC¥¶”√≤‚Ω«“«≤‚µ√ƒ¶ÃϬ÷◊Ó∏þµ„Aµƒ—ˆΩ«Œ™45°„£¨≤‚µ√‘≤–ƒOµƒ—ˆΩ«Œ™30°„£¨«Ûƒ¶ÃϬ÷µƒ∞Îæ∂£Æ£®Ω·π˚±£¡Ù∏˘∫≈£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com