
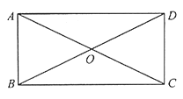
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD是矩形;
(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
【答案】(1)证明见解析;(2)∠ADO==36°.
【解析】
(1)先判断四边形ABCD是平行四边形,继而根据已知条件推导出AC=BD,然后根据对角线相等的平行四边形是矩形即可;
(2)设∠AOB=4x,∠ODC=3x,则∠OCD=∠ODC=3x.,在△ODC中,利用三角形内角和定理求出x的值,继而求得∠ODC的度数,由此即可求得答案.
(1)∵AO=OC,BO=OD,
∴四边形ABCD是平行四边形,
又∵∠AOB=2∠OAD,∠AOB是△AOD的外角,
∴∠AOB=∠OAD+∠ADO.
∴∠OAD=∠ADO.
∴AO=OD.
又∵AC=AO+OC=2AO,BD=BO+OD=2OD,
∴AC=BD.
∴四边形ABCD是矩形.
(2)设∠AOB=4x,∠ODC=3x,则∠ODC=∠OCD=3x,
在△ODC中,∠DOC+∠OCD+∠CDO=180°
∴4x+3x+3x=180°,解得x=18°,
∴∠ODC=3×18°=54°,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADO=∠ADC-∠ODC=90°-54°=36°.


科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
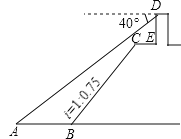
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
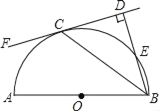
【题目】如图,AB是半圆O的直径,C是半圆O上的一点,CF切半圆O于点C,BD⊥CF于为点D,BD与半圆O交于点E.
(1)求证:BC平分∠ABD.
(2)若DC=8,BE=4,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
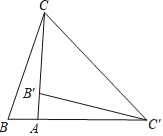
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CECA.
(1)求证:BC=CD;
(2)分别延长AB,DC交于点P,若PB=OB,CD=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
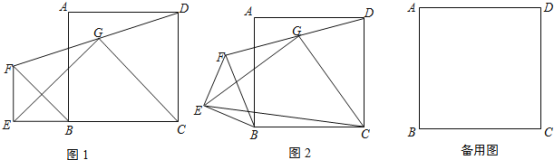
【题目】四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC.
(1)如图1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及![]() 的值;
的值;
(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,![]() ,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com