
| A. | 12 | B. | 18 | C. | 24 | D. | 40 |
分析 利用频率估计概率,可得到摸到红球的概率为$\frac{20}{60}$=$\frac{1}{3}$,设袋中有绿球x个数,于是根据概率公式得到$\frac{6}{x+6}$=$\frac{1}{3}$,然后解方程求出x即可.
解答 解:根据题意,小颖从中随机摸出一球,摸到红球的概率为$\frac{20}{60}$=$\frac{1}{3}$,
设袋中有绿球x个数,则$\frac{6}{x+6}$=$\frac{1}{3}$,解得x=12,
所以可估计袋中有绿球12个.
故选A.
点评 本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=5,b=6 | B. | a=1,b=-6 | C. | a=-1,b=-6 | D. | a=5,b=-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“ ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条)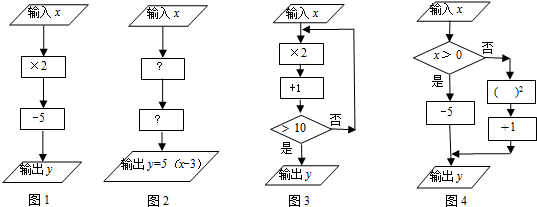
 ”内,应填-3;第二个运算框“
”内,应填-3;第二个运算框“ ”内,应填×5;
”内,应填×5;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com