
分析 先根据勾股定理,得圆心距的两部分分别是$\sqrt{21}$,$\sqrt{5}$,然后根据两圆的位置关系确定圆心距.
解答 解:如图,AB=4cm,O1A=5cm,O2A=4cm,
∵公共弦长为4cm,
∴AC=2cm,AC⊥O1O2,
∴O1C=$\sqrt{21}$cm,O2C=$\sqrt{5}$cm,
则如图1所示,当公共弦在两个圆心之间时,圆心距=$\sqrt{21}$+$\sqrt{5}$cm;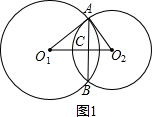
如图2所示,当公共弦在圆心的同侧时,圆心距=$\sqrt{21}$-$\sqrt{5}$cm.
故答案为$\sqrt{21}$±$\sqrt{5}$cm.
点评 此题综合运用了相交两圆的性质以及勾股定理.注意此题应考虑两种情况.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 9000(单位) | B. | 8000(单位) | C. | 1000(单位) | D. | 18000(单位) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
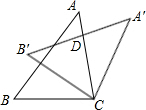 如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )| A. | 48° | B. | 58° | C. | 68° | D. | 78° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
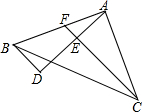 如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )
如图,在△ABC中,∠BAC=90°,AB=AC,AD是经过A点的一条直线,且B、C在AD的两侧,BD⊥AD于D,CE⊥AD于E,交AB于点F,CE=10,BD=4,则DE的长为( )| A. | 6 | B. | 5 | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com