
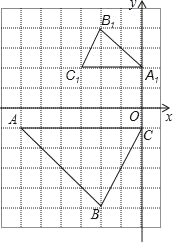
【题目】如图,△ABC与△A1B1C1是位似图形.
(1)在网格上建立平面直角坐标系,使得点A的坐标为(﹣6,﹣1),点C1的坐标为(﹣3,2),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
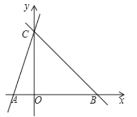
【题目】如图,直线y=kx+k交x轴,y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45.
(1)求直线BC的解析式;
(2)动点P从A出发沿射线AB匀速运动,速度为2个单位/秒,连接CP,设△PBC的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式,直接写出t的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
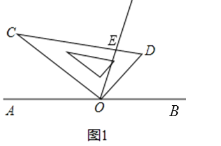
【题目】如图,点![]() 是直线
是直线![]() 上的一点,将一直角三角板如图摆放,过点
上的一点,将一直角三角板如图摆放,过点![]() 作射线
作射线![]() 平分
平分![]() .当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现
.当直角三角板绕点O继续顺时针旋转一周回到图1的位置时,在旋转过程中你发现![]() 与
与![]() 之间有怎样的数量关系?
之间有怎样的数量关系?
(1)如图1,当![]() 时,若
时,若![]() ,求
,求![]() 的度数;
的度数;
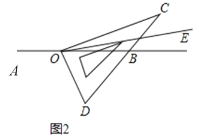
(2)如图2,当![]() 是钝角时,使得直角边
是钝角时,使得直角边![]() 在直线
在直线![]() 的上方,若
的上方,若![]() ,其他条件不变,直接写出
,其他条件不变,直接写出![]() 的度数;
的度数;
(3)若![]() ,在旋转过程中你发现
,在旋转过程中你发现![]() 与
与![]() 之间有怎样的数量关系?请你直接用含
之间有怎样的数量关系?请你直接用含![]() 的代数式表示
的代数式表示![]() 的度数;
的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市决定购进甲、乙两种取暖器,已知甲种取暖器每台进价比乙种取暖器多500元, 用40000元购进甲种取暖器的数量与用30000元购进乙种取暖器的数量相同.请解答下列问题:
(1)求甲、乙两种取暖器每台的进价;
(2)若甲种取暖器每台售价2500元,乙种取暖器每台售价1800元,超市欲同时购进两种取暖器20 台,且全部售出.设购进甲种取暖器x(台),所获利润为y(元),试用关于x的式子表示y;
(3)在(2)的条件下,若超市计划用不超过36000元购进取暖器,且甲种取暖器至少购进10台, 并将所获得的最大利润全部用于为某敬老院购买1100元/台的A型按摩器和700元/台的B型按摩器. 求购买按摩器的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
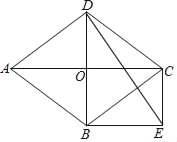
【题目】如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.
(1)求证:四边形OBEC是矩形;
(2)当∠ABD=60°,AD=2![]() 时,求∠EDB的正切值.
时,求∠EDB的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ABCD 的对角线 AC 、 BD 相交于点O , BD 12cm , AC 6cm ,点 E 在线段 BO 上从点 B 以1cm / s 的速度向点 O 运动,点 F 在线段OD 上从点O 以 2cm / s 的速度向点 D 运动.
(1)若点 E 、F 同时运动,设运动时间为t 秒,当t 为何值时,四边形 AECF 是平行四边形.
(2)在(1)的条件下,当 AB 为何值时, AECF 是菱形;
(3)求(2)中菱形 AECF 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO =45°.
(1)求A、B之间的路程;(参考数据: ![]() ,
, ![]() )
)
(2)请判断此校车是否超过了白田路每小时60千米的限制速度?

查看答案和解析>>
科目:初中数学 来源: 题型:
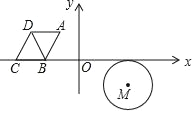
【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(3,﹣1),点A的坐标为(﹣2,![]() ),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,同时菱形ABCD沿x轴向右以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与BC相切,且切点为BC的中点时,连接BD,求:
①t的值;
②∠MBD的度数;
(3)在(2)的条件下,当点M与BD所在的直线的距离为1时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.

(1)求CD与AB之间的距离;
(2)某人从车站A出发,沿折线A→D→C→B去超市B.求他沿折线A→D→C→B到达超市比直接横穿马路多走多少米.
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com