
如图, ΔABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F。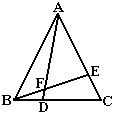
(1)求证:ΔABD≌ΔBCE.
(2)ΔAEF与ΔABE相似吗?请说明理由.
(3)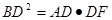 成立吗?请说明理由.
成立吗?请说明理由.
(1)证明∵ΔABC是等边三角形∴AB=BC,∠ABD=∠CBE=60°∵BD=CE∴ΔABD≌ΔBCE
(2)相似,两个三角形三组对应角对应相等,两三角形相似。
(3)成立。如果两三角形相似,那么这两个三角形对应边的比相等。
解析试题分析:(1)证明:∵ΔABC是等边三角形
∴AB=BC,∠ABD=∠CBE=60°
∵BD=CE
∴ΔABD≌ΔBCE
(2) ΔAEF与ΔABE相似
∵ΔABD≌ΔBCE
∴∠BAD=∠CBE
∵∠BAC=∠CBA=60°
∴∠ABE=∠FAE
∵∠AFE=∠BAD+∠ABE
∴∠AFE=∠CBE+∠ABE=∠CBA
∴ΔAEF∽ΔABE
(3) 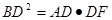 成立
成立
∵∠BAD=∠CBE, ∠ADB=∠BDF
∴ΔBDF∽ΔADB
∴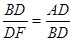
∴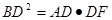
考点:全等及相似三角形
点评:本题难度中等,主要考查学生对全等三角形和相似三角形判定的学习。要证明两个三角形全等,可以用到“边角边,角边角,边边边定理”等,而相似三角形只需要求证两三角形两组对应角相等或两组对应边比值相等。熟练掌握全等及相似三角形的判定定理,是解这类题型的关键。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
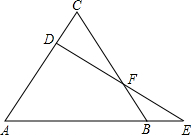 如图,△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连接DE交BC于F.
如图,△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连接DE交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连接BD并延长与CE交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:

| CE |
| CD |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com