练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，点E、F分别是□ABCD的边BC、AD上的点，且BE=DF．

    （1） 求证：四边形AECF是平行四边形；

    （2） 若AE=BE，∠BAC＝90°，试判断四边形AECF的形状，并说明理由．


    (1)   证明：在平行四边形ABCD中，AD//BC且AD=BC，（1分）

                     因BE=DF，所以AF=CE

                      \AF=CE且AF//CE

                      \四边形AECF是平行四边形．（3分）

    (2)  猜想： 四边形AECF是菱形        （4分）

    证明：∵AE=BE，\ÐEAB=ÐEBA

          ∵ÐBAC=900，\ÐCBA+ÐBCA=Ð=900．

                   \ÐEAC=ÐBAC

              \AE=BE=CE           （5分）

            \四边形AECF是菱形．   （6分）


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     如图，点C、F在BE上，∠ 1=∠ 2，BC=EF，请补充条件         ，使⊿ ABC≌⊿ DEF.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


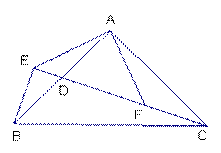
    如图，在△ABC中，∠BAC=90°，AB=AC，点D是AB的中点，连接CD，过B作BE⊥CD交CD的延长线于点E，连接AE，过A作AF⊥AE交CD于点F.

    （1）求证：AE=AF；  （2）求证：CD=2BE+DE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知弦AB的长等于⊙O的半径，弦AB所对的圆心角是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解方程：

    m2＋3m－1＝0    

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在− ， ，，0.3030030003，− ，3.14中，无理数的个数是  (     )

        A．2个          B．3个          C．4个          D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在平面直角坐标系xOy中，已知点P（2，2），点Q在y轴上，△PQO是等腰三角形，则满足条件的点Q共有         （    ）

    A．5个          B．4个              C．3个              D．2个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    问题背景：在△ABC中，AB、BC、AC三边的长分别为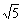、、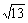，求这个三角形BC边上的高．

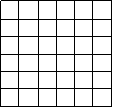
    杰杰同学在解答这道题时，先建立一个正方形网格(每个小正方形的边长为1)，再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处)．借用网格等知识就能计算出这个三角形BC边上的高．

    (1)请在正方形网格中画出格点△ABC；(2)求出这个三角形BC边上的高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （1）某冷库温度是零下10 ℃，下降-3 ℃后又下降5 ℃，两次变化后冷库温度是多少？

    （2）零下12 ℃比零上12 ℃低多少？

    （3）数轴上A、B两点表示的有理数分别是-6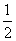 和7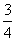，求A、B两点的距离.

    查看答案和解析>>

    同步练习册答案