
【题目】 如图1:已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,以
两点,以![]() 为直角顶点在第一象限内做等腰Rt△
为直角顶点在第一象限内做等腰Rt△![]() .
.

(1)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)求![]() 所在直线的函数关系式;
所在直线的函数关系式;
(3)如图2,直线![]() 交
交![]() 轴于点
轴于点![]() ,在直线
,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,
,![]() 与
与![]() 轴相交于点
轴相交于点![]() .
.
①求证:![]() ;
;
②在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使△
,使△![]() 的面积等于△
的面积等于△![]() 的面积?若存在,直接写出点
的面积?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)A(0,2),B(1,0);(2)直线BC所在直线解析式为y=![]() x-
x-![]() .(3)①证明见解析;②点P的坐标为(
.(3)①证明见解析;②点P的坐标为(![]() ,0)或(-
,0)或(-![]() ,0).
,0).
【解析】
(1)y=-2x+2中求出x=0时y的值和y=0时x的值即可得;
(2)作CD⊥x轴,证△ABO≌△BCD得BD=OA=2,CD=OB=1,据此可得C(3,1),再根据待定系数法求解可得;
(3)①作CG⊥x轴,EM⊥x轴,EN⊥y轴,先证△BCG≌△BEM得BM=BG=2,EM=CG=1,进一步求得OM=EN=OB=1,再证△BDO≌△EDN得BD=ED;
②作EH⊥x轴,先求出S△ABD=![]() ADOB=
ADOB=![]() ,再求出直线AE解析式为y=3x+2,得到F(-
,再求出直线AE解析式为y=3x+2,得到F(-![]() ,0),设P(a,0),知PF=|-
,0),设P(a,0),知PF=|-![]() -a|,依据S△APE=S△APF+S△EPF=
-a|,依据S△APE=S△APF+S△EPF=![]() PF(EH+AO)=
PF(EH+AO)=![]() |
|![]() +a|,根据S△ABD=S△APE得出关于a的方程,解之可得答案.
+a|,根据S△ABD=S△APE得出关于a的方程,解之可得答案.
(1)y=-2x+2中,当x=0时y=2,
则A(0,2),
当y=0时,-2x+2=0,解得x=1,
则B(1,0);
(2)如图①,过点C作CD⊥x轴于点D,
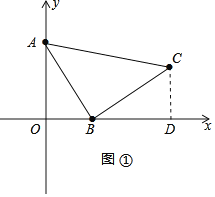
则∠AOB=∠BDC=90°,
∴∠OAB+∠ABO=90°,
∵△ABC是等腰直角三角形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBD=90°,
∴∠OAB=∠DBC,
∴△ABO≌△BCD(AAS),
∴BD=OA=2,CD=OB=1,
则点C(3,1),
设直线BC所在直线解析式为y=kx+b,
将点B(1,0)、C(3,1)代入,得:![]() ,
,
解得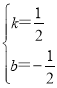 ,
,
∴直线BC所在直线解析式为y=![]() x-
x-![]() .
.
(3)①过点C作CG⊥x轴于点G,作EM⊥x轴于点M,EN⊥y轴于点N,
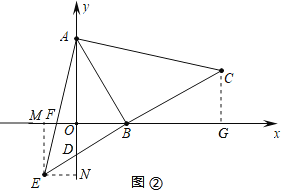
则∠BGC=∠BME=∠END=∠BOD=90°,
∵∠ABC=90°,且AE=AC,
∴AB是CE的中垂线,
∴BC=BE,
∵∠CBG=∠EBM,
∴△BCG≌△BEM(AAS),
∴BM=BG=2,EM=CG=1,
∵BO=1,
∴OM=EN=OB=1,
∵∠BDO=∠EDN,
∴△BDO≌△EDN(AAS),
∴BD=ED;
②如图③,作EH⊥x轴于点H,
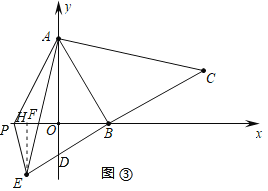
由y=![]() x-
x-![]() 知D(0,-
知D(0,-![]() ),即OD=
),即OD=![]() ,
,
则AD=OA+OD=![]() ,
,
∴S△ABD=![]() ADOB=
ADOB=![]() ×
×![]() ×1=
×1=![]() ,
,
由①知E(-1,-1),
根据A(0,2)、E(-1,-1)得直线AE解析式为y=3x+2,
当y=0时,3x+2=0,解得x=-![]() ,
,
∴F(-![]() ,0),
,0),
设P(a,0),
∴PF=|-![]() -a|,
-a|,
则S△APE=S△APF+S△EPF
=![]() PF(EH+AO)
PF(EH+AO)
=![]() |-
|-![]() -a|×3
-a|×3
=![]() |
|![]() +a|,
+a|,
∵S△ABD=S△APE,
∴![]() |
|![]() +a|=
+a|=![]() ,
,
解得a=![]() 或a=-
或a=-![]() ,
,
∴点P的坐标为(![]() ,0)或(-
,0)或(-![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,在半圆O中,直径AE=10,四边形ABCD是平行四边形,且顶点A、B、C在半圆上,点D在直径AE上,连接CE,若AD=8,则CE长为 .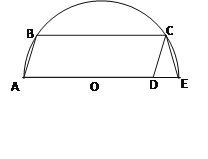
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是两块等边△ABC和等边△CDE的纸片叠放在一起的图形.
(1)如图2,固定△ABC,将△CDE绕点C按顺时针方向旋转30°,连接AD,BE,则线段BE,AD之间的大小关系如何?证明你的结论;
(2)如图3,若将△CDE绕点C按顺时针方向任意旋转一个角度(小于180°),连接AD,BE,则线段BE,AD之间大小关系如何?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC的平分线BE与∠ACB外角的平分线CE交于点E.
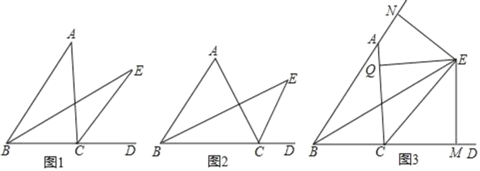
(1)如图1,若∠BAC=40°,则∠BEC= °
(2)如图2,将∠BAC变为60°,则∠BEC= °,写出∠BAC与∠BEC的关系;并说明你的理由
(3)在图1的基础上过点E分别作EN⊥BA于N,EQ⊥AC于Q,EM⊥BD于M,如图3,
求证:△ANE≌AQE,并求出∠NAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中,每个小格的顶点叫做格点.当所作正方形边上的点刚好在格点上的点称为整点.如图中![]() 四条边上的整点共有
四条边上的整点共有![]() 个;
个;![]() 四条边上的整点共有
四条边上的整点共有![]() 个.请你观察图中正方形
个.请你观察图中正方形![]() 四条边上的整点的个数…按此规律,推算出正方形
四条边上的整点的个数…按此规律,推算出正方形![]() 四条边上的整点共有________个.
四条边上的整点共有________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法研究函数![]() 的图象和性质,并解决问题.
的图象和性质,并解决问题.
![]() 完成下列步骤,画出函数
完成下列步骤,画出函数![]() 的图象;
的图象;
![]() 列表、填空;
列表、填空;
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
![]() 描点:
描点:
![]() 连线
连线
![]() 观察图象,当x______时,y随x的增大而增大;
观察图象,当x______时,y随x的增大而增大;
![]() 结合图象,不等式
结合图象,不等式![]() 的解集为______.
的解集为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com