
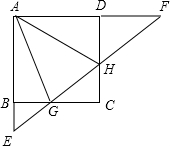
 如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.
如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.分析 (1)根据正方形ABCD的边长为4,BG=2,DH=3,可得CG=2,CH=1,再根据DF∥CG,得出△FDH∽△GCH,根据相似三角形的性质可得GH:HF的值,最后根据勾股定理的逆定理,判定△AGH是直角三角形,且∠AGH=90°即可;
(2)根据正方形ABCD的边长为4,BG=3,DH=1,得出CG=1,CH=3,再根据CG∥DF,CH∥BE,可得△CGH∽△BGE∽△DFH,最后根据相似三角形的性质以及勾股定理,求得DF、EG的长;
(3)根据正方形ABCD的边长为4,BG=x,DH=y,得出CG=4-x,CH=4-y,由(1)可得,△FDH∽△GCH,而△ABG∽△FDH,进而得出△ABG∽△GCH,根据相似三角形的对应边成比例,可得y与x之间的函数关系式为:y=$\frac{1}{4}$x2-x+4,最后运用二次函数的性质求得3≤y<4即可.
解答  解:(1)∵正方形ABCD的边长为4,BG=2,DH=3,
解:(1)∵正方形ABCD的边长为4,BG=2,DH=3,
∴CG=2,CH=1,
∵DF∥CG,
∴△FDH∽△GCH,
∴$\frac{GH}{FH}$=$\frac{CH}{DH}$=$\frac{1}{3}$,
∵Rt△GCH中,GH2=CG2+CH2=5,
Rt△ABG中,AG2=AB2+BG2=20,
Rt△ADH中,AH2=AD2+DH2=25,
∴GH2+AG2=AH2,
∴△AGH是直角三角形,且∠AGH=90°.
故答案为:1:3,90;
(2)∵正方形ABCD的边长为4,BG=3,DH=1,
∴CG=1,CH=3,
∵CG∥DF,CH∥BE,
∴△CGH∽△BGE∽△DFH,
∴$\frac{GC}{HC}$=$\frac{BG}{BE}$=$\frac{DF}{DH}$,即$\frac{1}{3}$=$\frac{3}{BE}$=$\frac{DF}{1}$,
解得BE=9,DF=$\frac{1}{3}$,
∴Rt△BEG中,EG=$\sqrt{B{G}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{9}^{2}}$=3$\sqrt{10}$;
(3)∵正方形ABCD的边长为4,BG=x,DH=y,
∴CG=4-x,CH=4-y,
由(1)可得,△FDH∽△GCH,而△ABG∽△FDH,
∴△ABG∽△GCH,
∴$\frac{AB}{GC}$=$\frac{BG}{CH}$,即$\frac{4}{4-x}$=$\frac{x}{4-y}$,
∴y与x之间的函数关系式为:y=$\frac{1}{4}$x2-x+4,
∵$\frac{4}{4-x}$=$\frac{x}{4-y}$,
∴4-y=$\frac{x(4-x)}{4}$=-$\frac{1}{4}{x}^{2}$+x,
∴当x=-$\frac{1}{2×(-\frac{1}{4})}$=2时,4-y有最大值,且最大值为-$\frac{1}{4}$×4+2=1,
∴0<4-y≤1,
解得3≤y<4.
点评 本题属于相似形综合题,主要考查了相似三角形的判定与性质、勾股定理及其逆定理,正方形的性质以及二次函数的性质的综合应用,解决问题的关键是运用相似三角形的对应边成比例,列出比例式进行求解.确定一个二次函数的最值时,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-(x+2)2 | B. | y=-(x-2)2 | C. | y=-x2-1 | D. | y=-x2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | M>N | B. | M<N | C. | M=N | D. | M≥N |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com