
����Ŀ��Ϊӭ��2016���п���ij��ѧ��ȫУ���꼶ѧ��������һ����ѧģ�⿼�ԣ��������ȡ�˲���ѧ���IJ��Գɼ���Ϊ�������з��������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ���ṩ����Ϣ����������⣺
��1����ε����У�һ����ȡ�˶�����ѧ����
��2���������б�ʾ�ɼ�Ϊ���С�����������������ͳ��ͼ����������
��3����ѧУ���꼶����1000�˲μ��������ѧ���ԣ����Ƹ�У���꼶���ж�����ѧ������ѧ�ɼ����Դﵽ���㣿
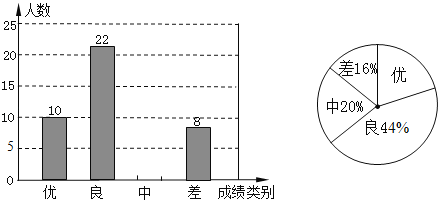
���𰸡���1��һ����ȡ��50��ѧ���� ��2��10�ˣ�ͳ��ͼ����������3����У���꼶����200��ѧ������ѧ�ɼ����Դﵽ����
��������
��1������ͳ��ͼ������ñ��ε����ѧ������
��2�����ݣ�1���еĽ����ͳ��ͼ�е����ݿ�����á��С���ѧ�������Ӷ����Խ�����ͳ��ͼ����������
��3������ͳ��ͼ������ø�У���꼶���ж�����ѧ������ѧ�ɼ����Դﵽ���㣮
����𡿽⣺��1��22��44%��50��
����ε����У�һ����ȡ��50��ѧ����
��2��50��20%��10��
��ȫ������ͳ��ͼ����ͼ��ʾ��
��3��1000��![]() ��200��
��200��
����У���꼶����200��ѧ������ѧ�ɼ����Դﵽ���㣮
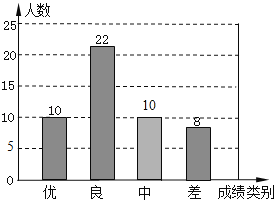


 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() ��
��![]() ����������
����������![]() ����
����![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ʱ����1��������
ʱ����1��������![]() ��
��![]() ��Ľ���Ϊ
��Ľ���Ϊ![]() ��
��![]() �������������ƣ�
�������������ƣ�
��1����![]() ��
��![]() ��ֵ��������
��ֵ��������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��������![]() �Ķ���
�Ķ���![]() ������Ϊ�� �� �����������ƣ���
������Ϊ�� �� �����������ƣ���![]() ��������
��������![]() �Ķ���
�Ķ���![]() ������Ϊ�� �� �������������ߵĶ�����������ĺ�����ϵʽ�� ��
������Ϊ�� �� �������������ߵĶ�����������ĺ�����ϵʽ�� ��
��3��̽�����н��ۣ�
���Ƿ����������![]() ��ʹ��
��ʹ��![]() Ϊ����ֱ�������Σ������ڣ�����������ߵı���ʽ���������ڣ���˵�����ɣ�
Ϊ����ֱ�������Σ������ڣ�����������ߵı���ʽ���������ڣ���˵�����ɣ�
����ֱ��![]() ��������
��������![]() �ֱ������߶�
�ֱ������߶�![]() ��
��![]() ����
����![]() ���߶�
���߶�![]() ��
��![]() ����
����![]() �ij��кι��ɣ����ú�
�ij��кι��ɣ����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
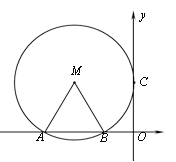
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���M�������ǣ�-2��![]() ������M��y�������ڵ�C����x���ཻ��A��B���㣮
������M��y�������ڵ�C����x���ཻ��A��B���㣮
(1)֤������MAB�ǵȱ������Σ�
(2)����M���Ƿ���ڵ�D��ʹ��ACD��ֱ�������Σ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
(3)��P��m��n���ǹ�A��B��C�������������һ�㣬����APB��30��ʱ��ֱ��д��m��ȡֵ��Χ��
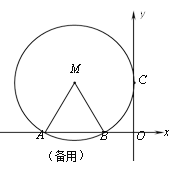
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
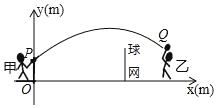
����Ŀ����ͼ�Ǽס������˽�����ë����ϰ��ʱ��һ��˲�䣬��ë����еĸ߶�y��m����ˮƽ����x��m����·��Ϊ�����ߵ�һ���֣���ͼ������O�����Ϸ�1m��P������һ����֪��O��������ˮƽ����Ϊ5m�������ĸ߶�Ϊ1.55m����ë����ˮƽ�����˶�4mʱ���ﵽ��ë�����������߶���![]() m��
m��
��1������ë����·�߶�Ӧ�ĺ�����ϵʽ��
��2��ͨ�������жϴ����ܷ������
��3���������������ë����е������ĸ߶�Ϊ![]() m��Q��ʱ���ҿ���ɹ����ʱ����������ˮƽ���룮
m��Q��ʱ���ҿ���ɹ����ʱ����������ˮƽ���룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽�ȫУѧ���Ե��ӽ�Ŀ��ϲ�����(���š����������������֡�Ϸ��),��ȫУѧ���������ȡ����ѧ�������ʾ����飬���ѵ��������Ƴ�������������ͳ��ͼ.
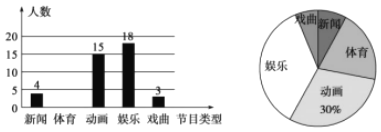
�����������Ϣ,�����������:
(1)��α������ѧ�����ж�����?
(2)�뽫����ͳ��ͼ��������;
(3)����УԼ��1500��ѧ��,����ȫУѧ����ϲ�����ֽ�Ŀ���ж�����?
(4)��У�㲥վ��Ҫ�㲥Ա,�־�����ϲ�����Ž�Ŀ�ļס��ҡ�����������ͬѧ��ѡȡ2��,��ǡ��ѡ�мס�����λͬѧ�ĸ���(����״ͼ���б������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
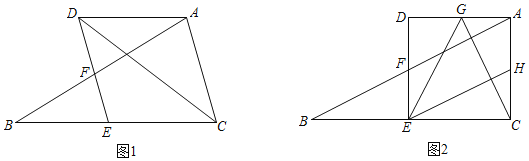
����Ŀ���ڡ�ABC�У���A��BC��ƽ���ߣ�����ACB��ƽ�����ڵ�D����E��BC��һ�㣬����DE����AB�ڵ�F����DEB+��CAD��180�㣮
��1����ͼ1����֤���ı���ACED�����Σ�
��2����ͼ2��G��AD���е㣬H��AC���е㣬����CG��EG��EH������ACB��90�㣬BC��2AC���ڲ������κθ����ߵ�����£���ֱ��д��ͼ�����CEHȫ�ȵ������Σ�������CEH��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ӱ��˾����ռ���2000����Ӱ���й����ݣ������������õ������
��Ӱ���� | ��һ�� | �ڶ��� | ������ | ������ | ������ | ������ |
��Ӱ���� | 140 | 50 | 300 | 200 | 800 | 510 |
������ |
|
|
|
|
|
|
ע����������ָһ���Ӱ�л�ú����IJ���������Ӱ�IJ����ı�ֵ��
![]() �����Ӱ��˾���ռ��ĵ�Ӱ�����ѡȡ1������ô�鵽���ⲿ��Ӱ�ǻ�ú����ĵ������Ӱ�ĸ�����______��
�����Ӱ��˾���ռ��ĵ�Ӱ�����ѡȡ1������ô�鵽���ⲿ��Ӱ�ǻ�ú����ĵ������Ӱ�ĸ�����______��
![]() ��Ӱ��˾Ϊ������Ͷ�ʻر�����ı�Ͷ�ʲ��ԣ��⽫���²�ͬ���͵�Ӱ�ĺ����ʷ����仯
��Ӱ��˾Ϊ������Ͷ�ʻر�����ı�Ͷ�ʲ��ԣ��⽫���²�ͬ���͵�Ӱ�ĺ����ʷ����仯![]() ���������ֻ�������Ӱ�ĺ��������ݷ����仯����ô�����Ӱ�ĺ���������
���������ֻ�������Ӱ�ĺ��������ݷ����仯����ô�����Ӱ�ĺ���������![]() �������Ӱ�ĺ����ʼ���
�������Ӱ�ĺ����ʼ���![]() ����ʹ�ı�Ͷ�ʲ��Ժ��ܵĺ����ʴﵽ���
����ʹ�ı�Ͷ�ʲ��Ժ��ܵĺ����ʴﵽ���
��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ��һ��P����O���������ߣ��е�ֱ�ΪA��B������AB����AB��PB��PA�Ϸֱ�ȡһ��D��E��F��ʹAD��BE��BD��AF������DE��DF��EF�����EDF���ڣ�������
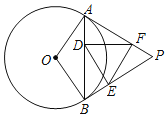
A.90�㩁��PB.90�㩁![]() ��PC.180�㩁��PD.45�㩁
��PC.180�㩁��PD.45�㩁![]() ��P
��P
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��![]() ��˫����
��˫����![]() ��x>0�����ڵ�
��x>0�����ڵ�![]() ��
��

��1����a��k��ֵ��
��2����ֱ֪��![]() ����
����![]() ��ƽ����ֱ��
��ƽ����ֱ��![]() ����P��m��n����m>3����ֱ��
����P��m��n����m>3����ֱ��![]() ��һ���㣬����P�ֱ���
��һ���㣬����P�ֱ���![]() �ᡢ
�ᡢ![]() ���ƽ���ߣ���˫����
���ƽ���ߣ���˫����![]() ��x>0���ڵ�
��x>0���ڵ�![]() ��
��![]() ��˫�����ڵ�M��N֮��IJ������߶�PM��PN��Χ�ɵ��������߽磩��Ϊ
��˫�����ڵ�M��N֮��IJ������߶�PM��PN��Χ�ɵ��������߽磩��Ϊ![]() ���ᡢ�����궼�������ĵ�������㣮
���ᡢ�����궼�������ĵ�������㣮
�ٵ�![]() ʱ��ֱ��д������
ʱ��ֱ��д������![]() �ڵ������������������
�ڵ������������������![]() �ڵ��������������8�������ͼ����m��ȡֵ��Χ��
�ڵ��������������8�������ͼ����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com