
【题目】如图,![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() ,
,![]()

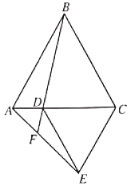

图1 图2 图3
(1)如图一,证明:![]()
(2)如图二,如果![]() 在
在![]() 边上,
边上,![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的度数.
的度数.
(3)如图三,在(2)的条件下,过![]() 作
作![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)10
;(3)10
【解析】
(1)先根据等边三角形的性质得出![]() ,再根据角的和差得出
,再根据角的和差得出![]() ,然后根据三角形全等的判定定理与性质即可得证;
,然后根据三角形全等的判定定理与性质即可得证;
(2)先根据三角形全等的判定定理与性质得出![]() ,再根据对顶角相等、三角形的外角性质即可得;
,再根据对顶角相等、三角形的外角性质即可得;
(3)如图(见解析),连接![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]() ,先根据等边三角形的判定与性质得出
,先根据等边三角形的判定与性质得出![]() ,再根据角的和差求出
,再根据角的和差求出![]() ,然后根据三角形全等的判定定理与性质得出
,然后根据三角形全等的判定定理与性质得出![]() ,最后根据线段的和差、直角三角形的性质求出
,最后根据线段的和差、直角三角形的性质求出![]() 的长,由此即可得出答案.
的长,由此即可得出答案.
(1)![]() 和
和![]() 均为等边三角形
均为等边三角形
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,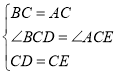
![]()
![]() ;
;
(2)![]() 和
和![]() 均为等边三角形
均为等边三角形
![]()
在![]() 和
和![]() 中,
中,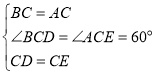
![]()
![]()
![]()
![]()
![]()
故![]() 的度数为
的度数为![]() ;
;
(3)如图,连接![]() ,在
,在![]() 上截取
上截取![]() ,连接
,连接![]()
由(2)可知:![]()
![]() 是等边三角形
是等边三角形
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,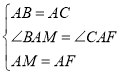
![]()
![]()
![]()
![]()
由(2)可知:![]()
![]()
![]()
![]()
又![]()
![]()
![]() ,即
,即![]()
![]()
![]()
![]()
即![]() 的长为10.
的长为10.



科目:初中数学 来源: 题型:
【题目】一个正方形AOBC各顶点的坐标分别为A(0,3),O(0,0),B(3,0),C(3,3).若以原点为位似中心,将这个正方形的边长缩小为原来的![]() ,则新正方形的中心的坐标为_____.
,则新正方形的中心的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
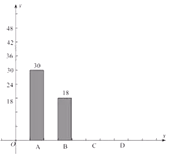
类型 | 频数 | 频率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
(1)学生共________人, ![]() ________,
________, ![]() ________;
________;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且sin∠DCB=![]() .
.
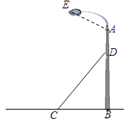
(1)求钢缆CD的长度。
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
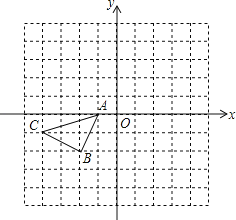
(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△A1B1C1.
(2)作△ABC关于坐标原点成中心对称的△A2B2C2.
(3)求B1的坐标 C2的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
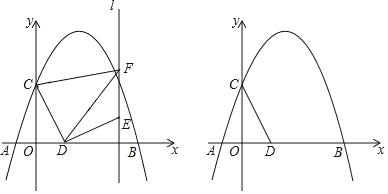
【题目】如图,抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com