
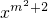 +(m-2)x-1=0提出了下列问题.
+(m-2)x-1=0提出了下列问题. =
= =1±
=1± ,
, ,x2=1-
,x2=1- .
. ,x2=1-
,x2=1- ;
; .
. .
. (b2-4ac≥0);用求根公式求解时,先要把方程化为一般式,确定a,b,c的值,计算出△=b2-4ac,然后代入公式.同时考查了一元二次方程和一元一次方程的定义以及分类讨论的思想的运用.
(b2-4ac≥0);用求根公式求解时,先要把方程化为一般式,确定a,b,c的值,计算出△=b2-4ac,然后代入公式.同时考查了一元二次方程和一元一次方程的定义以及分类讨论的思想的运用. 

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
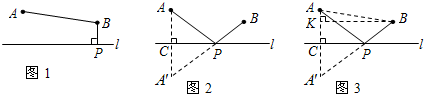
| a2+24 |
| a2+24 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:《28.2.1 解一元二次方程(公式法)》2010年习题精选(解析版) 题型:解答题
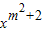 +(m-2)x-1=0提出了下列问题.
+(m-2)x-1=0提出了下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com