
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)

科目:初中数学 来源: 题型:
【题目】如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米,∠CAB=30°,∠CBA=45°,求AB的距离.(![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果取整数)
≈1.73,结果取整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.现将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2018次,点B的落点依次为![]() ,
,![]() ,
,![]() ,
,![]() , ……,则
, ……,则![]() 的坐标为________________.
的坐标为________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象经过点
的图象经过点![]() ,过点A作
,过点A作![]() 轴于点B,连结
轴于点B,连结![]() .
.
(1)求k的值;
(2)如图,若直线![]() 经过点A,与x轴相交于点C,且满足
经过点A,与x轴相交于点C,且满足![]() .求:
.求:
①直线![]() 的表达式;
的表达式;
②记直线![]() 与双曲线
与双曲线![]() 的另一交点为
的另一交点为![]() ,试求
,试求![]() 的面积
的面积![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0), B(0,﹣1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A20的坐标为 ( )
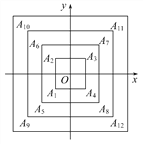
A. (5,5) B. (5,-5) C. (-5,5) D. (-5,-5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com