
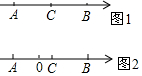
 如图1,在数轴上,A点、B点与C点的距离相等.
如图1,在数轴上,A点、B点与C点的距离相等.分析 (1)根据A、B的坐标和AC=BC得出即可;
(2)根据A、B的坐标得出即可;
(3)求出a<0<c<b,|b|>|a|>|c|,由(2)得:a+b=2c,求出a-2c=-b,b-2c=-a,a+b-2c,=0,去掉绝对值符号,即可得出答案.
解答 解:(1)∵在数轴上,A点、B点与C点的距离相等,A点、B点表示的数分别为3,9,
∴C表示的数是6,
故答案为:6;
(2)∵A点、B点表示的数分别为m,n,
∴C点表示的数是$\frac{m+n}{2}$,
故答案为:$\frac{m+n}{2}$;
(3)∵从数轴可知:a<0<c<b,|b|>|a|>|c|,
由(2)得:a+b=2c,
∴a-2c=a-(a+b)=-b,b-2c=b-(a+b)=-a,
a+b-2c=2c-2c=0,
∴|a+b|-|a-2c|+|b-2c|-|a+b-2c|
=|a+b|-|-b|+|-a|-|0|
=a+b-b-a-0=0.
点评 本题考查了整式的加减,数轴,绝对值的应用,能正确去掉绝对值符号是解此题的关键.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题
 如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 A、B、C、D四位同事去茶馆喝茶,现A已入坐,B、C、D三人将随机坐到其余三个位置上.若A希望与D相邻而坐,那么他实现愿望的概率为多少?(要求画树状图列出所有的可能情况)
A、B、C、D四位同事去茶馆喝茶,现A已入坐,B、C、D三人将随机坐到其余三个位置上.若A希望与D相邻而坐,那么他实现愿望的概率为多少?(要求画树状图列出所有的可能情况)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了测量某大桥的桥塔高度AB,在与桥塔底部B相距50米的C处,用高1米的测角仪DC测得桥塔顶端A的仰角为41.5°,求桥塔AB的高度.(结果精确到0.1米)
如图,为了测量某大桥的桥塔高度AB,在与桥塔底部B相距50米的C处,用高1米的测角仪DC测得桥塔顶端A的仰角为41.5°,求桥塔AB的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,D是AB边上的一点,在下列三个关系:①∠ACB=90°;②AC=CD;③∠ACD=2∠B中,取两个作为题设,另一个作为结论,组成一个真命题,并写出证明过程.
如图,△ABC中,D是AB边上的一点,在下列三个关系:①∠ACB=90°;②AC=CD;③∠ACD=2∠B中,取两个作为题设,另一个作为结论,组成一个真命题,并写出证明过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com