
已知抛物线的解析式为
(1)求证:不论m为何值,此抛物线与x轴必有两个交点,且两交点A、B之间的距离为定值;
(2)设点P为此抛物线上一点,若△PAB的面积为8,求符合条件的点P的坐标;
(3)若(2)中△PAB的面积为S(S>0),试根据面积S值的变化情况,确定符合条件的点P的个数(本小题直接写出结论,不要求写出计算、证明过程).
(1)证明见解析;(2)(m,4)或(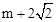 ,?4)或(
,?4)或(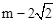 ,-4);(3)当s=8时,符合条件的点P有3个,当0<s<8时,符合条件的点P有4个,当s>8时,符合条件的点P有2个.
,-4);(3)当s=8时,符合条件的点P有3个,当0<s<8时,符合条件的点P有4个,当s>8时,符合条件的点P有2个.
解析试题分析:(1)本题需先求出△的值,再证出△>0,再设出A、B的坐标,然后代入公式即可求出AB的长;
(2)本题需先设出P的坐标,再由题意得出b的值,然后即可求出符合条件的所有点P的坐标;
(3)本题需分当s=8时,当0<s<8时,当s>8时三种情况进行讨论,即可得出符合条件的点P的个数.
试题解析::(1)∵△=(2m)2-4×(-1)(4-m2)=16>0,
∴不论m取何值,此抛物线与x轴必有两个交点.
设A(x1,0),B(x2,0),
则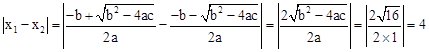 (定值).
(定值).
(2)设P(a,b),则由题意b=-a2+2am+4-m2,且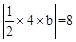 ,
,
解得b=±4.
当b=4时得:a=m,即P(m,4);
当b=-4时得: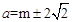 ,即P(
,即P(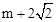 ,?4)或P(
,?4)或P(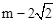 ,-4).
,-4).
综上所述,符合条件的点P的坐标为(m,4)或(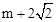 ,?4)或(
,?4)或(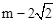 ,-4).
,-4).
(3)由(2)知当s=8时,符合条件的点P有3个,当0<s<8时,符合条件的点P有4个,当s>8时,符合条件的点P有2个.
考点:1.二次函数的和性质;2.曲线上点的坐标与方程的关系;3.分类思想的应用.


科目:初中数学 来源: 题型:解答题
如图在平面直角坐标系内,以点C(1,1)为圆心,2为半径作圆,交x轴于A、B两点,开口向下的抛物线经过A、B两点,且其顶点P在⊙C上。
(1)写出A、B两点的坐标;
(2)确定此抛物线的解析式;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系xOy中,二次函数 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.
(1)求此二次函数的解析式并画出二次函数图象;
(2)点P(t,0)是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,等边△ABC的边长为4,E是边BC上的动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).
(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线);
(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ的面积(用含 的代数式表示);
的代数式表示);
(3)当(2)中 的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某超市准备进一批每个进价为40元的小家电,经市场调查预测,售价定为50元时可售出400个;定价每增加1元,销售量将减少10个.
(1)设每个定价增加 元,此时的销售量是多少?(用含
元,此时的销售量是多少?(用含 的代数式表示)
的代数式表示)
(2)超市若准备获得利润6000元,并且使进货量较少,则每个应定价为多少元?
(3)超市若要获得最大利润,则每个应定价多少元?获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
李经理在某地以10元/千克的批发价收购了2 000千克核桃,并借一仓库储存.在存放过程中,平均每天有6千克的核桃损耗掉,而且仓库允许存放时间最多为60天.若核桃的市场价格在批发价的基础上每天每千克上涨0.5元。
(1)存放x天后,将这批核桃一次性出售,如果这批核桃的销售总金额为y元,试求出y与x之间的函数关系式;
(2)如果仓库存放这批核桃每天需要支出各种费用合计340元,李经理要想获得利润22 500元,需将这批核桃存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
平面直角坐标系xOy中,抛物线y=ax2-4ax+4a+c 与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
(1)求此抛物线的解析式;
(2)若点P是线段BC上的一个动点,过点P作y轴的平行线与抛物线在x轴下方交于点Q,试问线段PQ的长度是否存在最大值?若存在,求出其最大值;若不存在,请说明理由;
(3)若此抛物线的对称轴上的点M满足∠AMC=45°,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=- x2+bx+c的图象经过B、C两点.
x2+bx+c的图象经过B、C两点.
(1)求b,c的值.
(2)结合函数的图象探索:当y>0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:抛物线 与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
与x轴交于点A、B(A左B右),其中点B的坐标为(7,0),设抛物线的顶点为C.
(1)求抛物线的解析式和点C的坐标;
(2)如图1,若AC交y轴于点D,过D点作DE∥AB交BC于E.点P为DE上一动点,PF⊥AC于F,PG⊥BC于G.设点P的横坐标为a,四边形CFPG的面积为y,求y与a的函数关系式和y的最大值;
(3)如图2,在条件(2)下,过P作PH⊥x轴于点H,连结FH、GH,是否存在点P,使得△PFH与△PHG相似?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com