Question

如图，BD平分∠CDA，EB平分∠AEC，∠A＝27°，∠B=33°，则∠C=_____。

Answer 1

∠C＝39°

解析试题分析：连接DE，根据三角形的内角和定理及角平分线的性质可得∠A=180°-∠1-∠2-2∠BEC，∠B=180°-∠1-∠BDA-∠2-∠BEC，∠C=180°-∠1-∠2-2∠BDA，即可得到∠A+∠C=2∠B，从而可以求得结果.
连接DE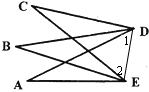

由题意得∠A=180°-∠1-∠AED=180°-∠1-∠2-∠AEC=180°-∠1-∠2-2∠BEC
∠B=180°-∠BDE-∠BED=180°-∠1-∠BDA-∠2-∠BEC
∠C=180°-∠2-∠CDE=180°-∠1-∠2-∠CDA=180°-∠1-∠2-2∠BDA
所以∠A+∠C=(180°-∠1-∠2-2∠BEC)+(180°-∠1-∠2-2∠BDA)
=2(180°-∠1-∠2-∠BEC-∠BDA)=2∠B
所以∠C=2∠B-∠A=2×33°-27°=39°.
考点：角平分线的性质，三角形的内角和定理
点评：角平分线的性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.