
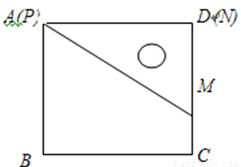
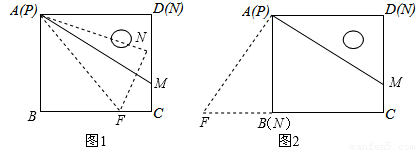
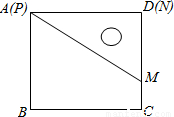
已知一个直角三角板PMN,∠MPN=30°,MN=2,使它的一边PN与正方形ABCD的一边AD重合(如图放置在正方形内)把三角板绕点P旋转,使点M落在直线BC上一点F处,则CF的长为______________.
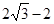 或
或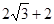 .
.
【解析】
试题分析:本题考查了旋转的性质、正方形的性质、以及解直角三角形.解答此题的关键也是难点在于区分△PMN的顶点不在直线BC上和在在直线BC上两种情况讨论求解.解直角三角形求出正方形的边长AD的长度,
由∠MPN=30°,MN=2,得AD=MN•cot∠MPN=2×cot30°=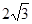 .然后分两种情况:①点F在BC上,点N不在BC上时,根据旋转的性质可得AF=AM,利用“HL”证明Rt△ABF和Rt△ADM全等,进而可得BF=DM,从而得到CF=CM=CD-DM=
.然后分两种情况:①点F在BC上,点N不在BC上时,根据旋转的性质可得AF=AM,利用“HL”证明Rt△ABF和Rt△ADM全等,进而可得BF=DM,从而得到CF=CM=CD-DM=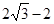 ;②点F、B都在直线BC上时,根据旋转的性质可得BF=MN=2,然后根据CF=BC+BF=
;②点F、B都在直线BC上时,根据旋转的性质可得BF=MN=2,然后根据CF=BC+BF=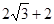 .所以CF的长为
.所以CF的长为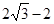 或
或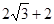 .
.
考点:1、旋转的性质;2、正方形的性质.


科目:初中数学 来源: 题型:
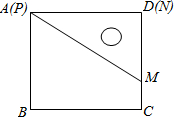 已知一个直角三角板PMN,∠MPN=30°,MN=2,使它的一边PN与正方形ABCD的一边AD重合(如图放置在正方形内)把三角板绕点P旋转,使点M落在直线BC上一点F处,则CF的长为
已知一个直角三角板PMN,∠MPN=30°,MN=2,使它的一边PN与正方形ABCD的一边AD重合(如图放置在正方形内)把三角板绕点P旋转,使点M落在直线BC上一点F处,则CF的长为| 3 |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河南信阳市二中中考模拟考试数学试卷(解析版) 题型:填空题
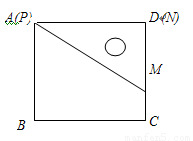
已知一个直角三角板PMN,∠MPN=30°,MN=2,使它的一边PN与正方形ABCD的一边AD重合(如图放置在正方形内)把三角板绕点P旋转,使点M落在直线BC上一点F处,则CF的长为 .
查看答案和解析>>
科目:初中数学 来源:2012年河南省信阳市二中中考数学模拟试卷(解析版) 题型:填空题
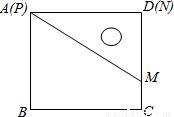
查看答案和解析>>
科目:初中数学 来源:2012年河南省中考数学模拟试卷(七)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com