
”¾ĢāÄæ”æČēĶ¼1£¬Į½øöµČŃüÖ±½ĒČż½Ē°åABCŗĶDEFÓŠŅ»Ģõ±ßŌŚĶ¬Ņ»ĢõÖ±ĻßlÉĻ£¬DE=2£¬AB=1£®½«Ö±ĻßEBČʵćEÄꏱÕėŠż×Ŗ45”ć£¬½»Ö±ĻßADÓŚµćM£®½«Ķ¼1ÖŠµÄČż½Ē°åABCŃŲÖ±ĻßlĻņÓŅĘ½ŅĘ£¬ÉčC”¢EĮ½µć¼äµÄ¾ąĄėĪŖk£®
½ā“šĪŹĢā£ŗ
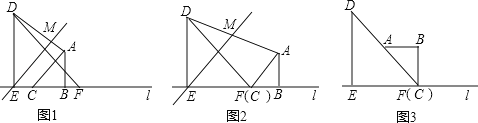
£Ø1£©¢Łµ±µćCÓėµćFÖŲŗĻŹ±£¬ČēĶ¼2ĖłŹ¾£¬æɵĆ![]() µÄÖµĪŖ £»
µÄÖµĪŖ £»
¢ŚŌŚĘ½ŅĘ¹ż³ĢÖŠ£¬![]() µÄÖµĪŖ £ØÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾£©£»
µÄÖµĪŖ £ØÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾£©£»
£Ø2£©½«Ķ¼2ÖŠµÄČż½Ē°åABCČʵćCÄꏱÕėŠż×Ŗ£¬ŌĢāÖŠµÄĘäĖūĢõ¼ž±£³Ö²»±ä£®µ±µćAĀäŌŚĻ߶ĪDFÉĻŹ±£¬ČēĶ¼3ĖłŹ¾£¬Ēė²¹Č«Ķ¼ŠĪ£¬¼ĘĖć![]() µÄÖµ£»
掙术
£Ø3£©½«Ķ¼1ÖŠµÄČż½Ē°åABCČʵćCÄꏱÕėŠż×Ŗ¦Į¶Č£¬0£¼¦Į”Ü90£¬ŌĢāÖŠµÄĘäĖūĢõ¼ž±£³Ö²»±ä£®¼ĘĖć![]() µÄÖµ£ØÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾£©£®
µÄÖµ£ØÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾£©£®
”¾“š°ø”æ£Ø1£©¢Ł![]() =1£»¢Ś
=1£»¢Ś![]() =
=![]() £»£Ø2£©
£»£Ø2£©![]() £®£Ø3£©
£®£Ø3£©![]() £®
£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©¢Łøł¾ŻĢāŅāæɵĆEM“¹Ö±Ę½·ÖDF£¬Ö±ĻßAF”ĪEM£¬“Ó¶ų![]() ×Ŗ»ÆĪŖ
×Ŗ»ÆĪŖ![]() £¬¼Ģ¶ųµĆ³ö½įĀŪ£»¢Ś·ĀÕÕ¢ŁµÄĖ¼Ā·½ųŠŠĒó½ā¼“æÉ£»
£¬¼Ģ¶ųµĆ³ö½įĀŪ£»¢Ś·ĀÕÕ¢ŁµÄĖ¼Ā·½ųŠŠĒó½ā¼“æÉ£»
£Ø2£©ĻČ²¹Č«Ķ¼ŠĪ£¬Į¬½ÓAE£¬·Ö±šĒó³öAM¼°DMµÄÖµ£¬Č»ŗóæÉČ·¶Ø±ČÖµ£®
£Ø3£©ĻČ»³öĶ¼ŠĪ£¬Č»ŗóÖ¤Ć÷”÷ABG”Õ”÷CBE£¬¼Ģ¶ųĶĘ³öAG”ĪDE£¬”÷AGM”×”÷DEM£¬ĄūÓĆĻąĖĘČż½ĒŠĪµÄŠŌÖŹ¼“æÉµĆ³ö“š°ø£®
½ā£ŗ£Ø1£©¢ŁČēĶ¼£¬
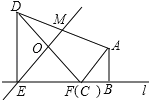
”ß”ĻMEB=45”ć£¬”ĻAFB=45”ć£¬
”ąEM“¹Ö±ĒŅĘ½·ÖDF£¬AF”ĪEM£¬
”ą![]() =
=![]() =1£»
=1£»
¢ŚČēĶ¼

ÓÉ¢ŁæɵĆ![]() =
=![]() =
=![]() =
=![]() =
=![]() £»
£»
£Ø2£©Į¬½ÓAE£¬
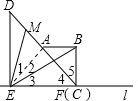
”ß”÷ABC£¬”÷DEF¾łĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬DE=2£¬AB=1£¬
”ąEF=2£¬BC=1£¬”ĻDEF=90”ć£¬”Ļ4=”Ļ5=45”ć
”ąDF=2![]() £¬AC=
£¬AC=![]() £¬”ĻEFB=90”ć£¬
£¬”ĻEFB=90”ć£¬
”ąDF=2AC£¬AD=![]() £¬
£¬
”ąµćAĪŖCDµÄÖŠµć£¬
”ąEA”ĶDF£¬EAĘ½·Ö”ĻDEF£¬
”ą”ĻMAE=90”ć£¬”ĻAEF=45”ć£¬AE=![]() £¬
£¬
”ß”ĻBEM=45”ć£¬
”ą”Ļ1+”Ļ2=”Ļ3+”Ļ2=45”ć£¬
”ą”Ļ1=”Ļ3£¬
”ą”÷AEM”×”÷FEB£¬
”ą![]() £¬
£¬
”ąAM=![]() £¬
£¬
”ąDM=AD©AM=![]() £¬
£¬
”ą![]() £®
£®
£Ø3£©¹żB×÷BEµÄ“¹Ļß½»Ö±ĻßEMÓŚµćG£¬Į¬½ÓAG”¢BG£¬
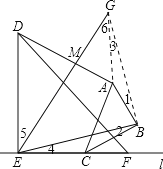 £¬
£¬
”ą”ĻEBG=90”ć£¬
”ß”ĻBEM=45”ć£¬
”ą”ĻEGB=”ĻBEM=45”ć£¬
”ąBE=BG£¬
”ß”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąBA=BC£¬”ĻABC=90”ć£¬
”ą”Ļ1=”Ļ2£¬
”ą”÷ABG”Õ”÷CBE£¬
”ąAG=EC=k£¬”Ļ3=”Ļ4£¬
”ß”Ļ3+”Ļ6=”Ļ5+”Ļ4=45”ć£¬
”ą”Ļ6=”Ļ5£¬
”ąAG”ĪDE£¬
”ą”÷AGM”×”÷DEM£¬
”ą![]() £®
£®


 Š”ѧ¶į¹ŚAB¾ķĻµĮŠ“š°ø
Š”ѧ¶į¹ŚAB¾ķĻµĮŠ“š°ø ABCæ¼ĶõČ«ÓžķĻµĮŠ“š°ø
ABCæ¼ĶõČ«ÓžķĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌÓŚŅ»øö¾ŲŠĪABCD¼°”ŃMøų³öČēĻĀ¶ØŅå£ŗŌŚĶ¬Ņ»Ę½ĆęÄŚ£¬Čē¹ū¾ŲŠĪABCDµÄĖÄøö¶„µćµ½”ŃMÉĻŅ»µćµÄ¾ąĄėĻąµČ£¬ÄĒĆ“³ĘÕāøö¾ŲŠĪABCDŹĒ”ŃMµÄ”°°éĀĀ¾ŲŠĪ”±£®ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±Ļßl£ŗ![]() ½»xÖįÓŚµćM£¬”ŃMµÄ°ė¾¶ĪŖ2£¬¾ŲŠĪABCDŃŲÖ±ĻßŌĖ¶Æ£ØBDŌŚÖ±ĻßlÉĻ£©£¬BD=2£¬AB”ĪyÖį£¬µ±¾ŲŠĪABCDŹĒ”ŃMµÄ”°°éĀĀ¾ŲŠĪ”±Ź±£¬µćCµÄ×ų±źĪŖ £®
½»xÖįÓŚµćM£¬”ŃMµÄ°ė¾¶ĪŖ2£¬¾ŲŠĪABCDŃŲÖ±ĻßŌĖ¶Æ£ØBDŌŚÖ±ĻßlÉĻ£©£¬BD=2£¬AB”ĪyÖį£¬µ±¾ŲŠĪABCDŹĒ”ŃMµÄ”°°éĀĀ¾ŲŠĪ”±Ź±£¬µćCµÄ×ų±źĪŖ £®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĢģŌē³æ£¬ÕÅĒæ“Ó¼ŅÅܲ½Č„ĢåÓż¶ĶĮ¶£¬Ķ¬Ź±ĀčĀč“ÓĢåÓż³”³æĮ·½įŹų»Ų¼Ņ£¬Ķ¾ÖŠĮ½ČĖĻąÓö£¬ÕÅĒæÅܵ½ĢåÓż³”ŗó·¢ĻÖŅŖĻĀÓź£¬Į¢¼“°“ŌĀ··µ»Ų£¬Óöµ½ĀčĀčŗóĮ½ČĖŅ»Ęš»Ųµ½¼Ņ£ØÕÅĒæŗĶĀčĀčŹ¼ÖÕŌŚĶ¬Ņ»Ģõ±ŹÖ±µÄ¹«Ā·ÉĻŠŠ×ߣ©£®ČēĶ¼ŹĒĮ½ČĖĄė¼ŅµÄ¾ąĄėy£ØĆ×£©ÓėÕÅĒæ³ö·¢µÄŹ±¼äx£Ø·Ö£©Ö®¼äµÄŗÆŹżĶ¼Ļó£¬øł¾ŻĶ¼ĻóŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĒóÕÅĒæ·µ»ŲŹ±µÄĖŁ¶Č£»
£Ø2£©ĀčĀč±Č°“ŌĖŁ·µ»ŲĢįĒ°¶ąÉŁ·ÖÖÓµ½¼Ņ£æ
£Ø3£©ĒėÖ±½ÓŠ“³öÕÅĒæÓėĀčĀčŗĪŹ±Ļą¾ą1200Ć×£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅŹŠ”°ÉĻĘ·”±·æµŲ²śæŖ·¢¹«Ė¾ÓŚ2010Äź5ŌĀ·ŻĶź¹¤Ņ»ÉĢĘ··æŠ”Ēų£¬6ŌĀ³õæŖŹ¼ĻśŹŪ£¬ĘäÖŠ6ŌĀµÄĻśŹŪµ„¼ŪĪŖ0.7ĶņŌŖ/m2£¬7ŌĀµÄĻśŹŪµ„¼ŪĪŖ0.72ĶņŌŖ/m2£¬ĒŅĆæŌĀĻśŹŪ¼Ūøńy1£Øµ„Ī»£ŗĶņŌŖ/m2£©ÓėŌĀ·Żx£Ø6”Üx”Ü11£¬xĪŖÕūŹż£©Ö®¼äĀś×ćŅ»“ĪŗÆŹż¹ŲĻµ£ŗĆæŌĀµÄĻśŹŪĆ껿ĪŖy2£Øµ„Ī»£ŗm2£©£¬ĘäÖŠy2=©2000x+26000£Ø6”Üx”Ü11£¬xĪŖÕūŹż£©£®
£Ø1£©Ēóy1ÓėŌĀ·ŻxµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©6”«11ŌĀÖŠ£¬ÄÄŅ»øöŌĀµÄĻśŹŪ¶ī×īøߣæ×īøßĻśŹŪ¶īĪŖ¶ąÉŁĶņŌŖ£æ
£Ø3£©2010Äź11ŌĀŹ±£¬Ņņ»įŹÜµ½¼“½«ŹµŠŠµÄ”°¹ś°ĖĢõ”±ŗĶ·æ²śĖ°Õž²ßµÄÓ°Ļģ£¬øĆ¹«Ė¾ĻśŹŪ²æŌ¤¼Ę12ŌĀ·ŻµÄĻśŹŪĆ껿»įŌŚ11ŌĀĻśŹŪĆ껿»ł“”ÉĻ¼õÉŁ20a%£¬ÓŚŹĒ¾ö¶Ø½«12ŌĀ·ŻµÄĻśŹŪ¼ŪøńŌŚ11ŌĀµÄ»ł“”ÉĻŌö¼Óa%£¬øĆ¼Ę»®Ė³ĄūĶź³É£®ĪŖĮĖ¾”æģŹÕ»Ų׏½š£¬2011Äź1ŌĀ¹«Ė¾½ųŠŠ½µ¼Ū“ŁĻś£¬øĆŌĀĻśŹŪ¶īĪŖ£Ø1500+600a£©ĶņŌŖ£®ÕāŃł12ŌĀ”¢1ŌĀµÄĻśŹŪ¶ī¹²ĪŖ4618.4ĶņŌŖ£¬Ēėøł¾ŻŅŌÉĻĢõ¼žĒó³öaµÄÖµĪŖ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅ¹ś¶Ō”°Ņ»“ųŅ»Ā·”±ŃŲĻß¹ś¼Ņ²»¶Ļ¼Ó“óĶ¶×Ź£¬ÄæĒ°ŅŃĪŖÓŠ¹Ų¹ś¼Ņ““ŌģĮĖ½ü1100000000 ĆĄŌŖĖ°ŹÕ£¬ĘäÖŠ1100000000 ÓĆæĘѧ¼ĒŹż·Ø±ķŹ¾Ó¦ĪŖ£Ø £©
A. 0.11108B. 1.11010C. 1.1109D. 11108
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČē¹ūĮćÉĻ6”ę¼Ē×÷ +6”ę£¬ÄĒĆ“ĮćĻĀ2”ę¼Ē×÷£Ø””””£©
A. -2 B. 2 C. -2”ę D. 2”ę
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖx=2ŹĒ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģax2-3bx-5=0µÄŅ»øöøł,Ōņ4a-6b+6µÄÖµŹĒ£Ø £©
A. 1 B. 6 C. 11 D. 12
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com